Pendule inversé : théorie du contrôle et dynamique : 17 étapes (avec images)

2024 Auteur: John Day | [email protected]. Dernière modifié: 2024-01-30 09:07

Le pendule inversé est un problème classique en théorie de la dynamique et du contrôle qui est généralement élaboré dans les cours de physique ou de mathématiques du secondaire et du premier cycle. Étant moi-même passionné de mathématiques et de sciences, j'ai décidé d'essayer de mettre en œuvre les concepts que j'ai appris pendant mes cours pour construire un pendule inversé. L'application de tels concepts dans la vie réelle aide non seulement à renforcer votre compréhension des concepts, mais vous expose également à une toute nouvelle dimension de problèmes et de défis liés à la pratique et aux situations de la vie réelle que l'on ne peut jamais rencontrer dans les cours théoriques.

Dans ce instructable, je vais d'abord présenter le problème du pendule inversé, puis couvrir l'aspect théorique du problème, puis discuter du matériel et des logiciels nécessaires pour donner vie à ce concept.

Je vous suggère de regarder la vidéo qui est jointe ci-dessus tout en parcourant l'instructable qui vous donnera une meilleure compréhension.

Et enfin, n'oubliez pas de voter pour le « Concours scientifique en classe » si vous avez aimé ce projet et n'hésitez pas à laisser vos questions dans la section des commentaires ci-dessous. Bonne fabrication !:)

Étape 1: Le problème

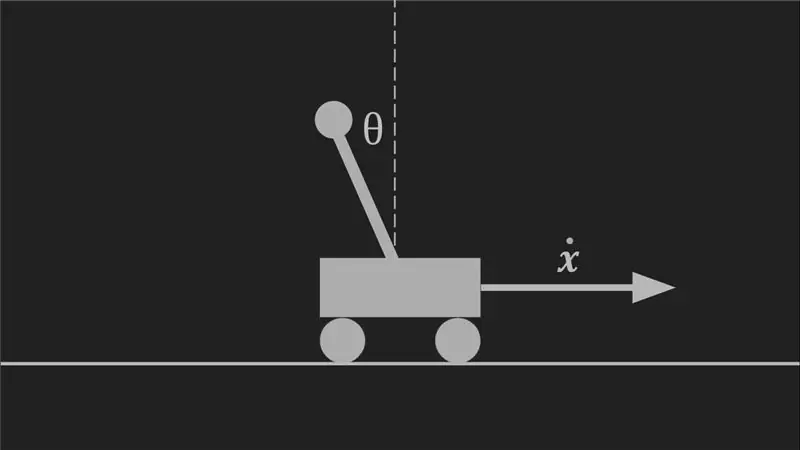
Le problème du pendule inversé est analogue à l'équilibre d'un balai ou d'une longue perche sur la paume de votre main, ce que la plupart d'entre nous avons essayé étant enfant. Lorsque nos yeux voient le poteau tomber d'un certain côté, ils envoient cette information au cerveau qui effectue certains calculs, puis demande à votre bras de se déplacer vers une certaine position avec une certaine vitesse pour contrer le mouvement du poteau, ce qui, espérons-le, amènerait le basculement du poteau à la verticale. Ce processus est répété plusieurs centaines de fois par seconde, ce qui garde le pôle complètement sous votre contrôle. Le pendule inversé fonctionne de manière similaire. L'objectif est d'équilibrer un pendule à l'envers sur un chariot que l'on laisse circuler. Au lieu des yeux, un capteur est utilisé pour détecter la position du pendule qui envoie les informations à un ordinateur qui effectue certains calculs et ordonne aux actionneurs de déplacer le chariot de manière à rendre le pendule à nouveau vertical.

Étape 2: la solution

Ce problème d'équilibrage d'un pendule à l'envers nécessite un aperçu des mouvements et des forces qui sont en jeu dans ce système. Finalement, cet aperçu nous permettra de proposer des "équations de mouvement" du système qui peuvent être utilisées pour calculer les relations entre la sortie qui va aux actionneurs et les entrées provenant des capteurs.

Les équations du mouvement peuvent être dérivées de deux manières selon votre niveau. Ils peuvent être dérivés soit en utilisant les lois fondamentales de Newton et quelques mathématiques de niveau secondaire, soit en utilisant la mécanique lagrangienne qui est généralement introduite dans les cours de physique de premier cycle. (Remarque: dériver les équations du mouvement à l'aide des lois de Newton est simple mais fastidieux alors que l'utilisation de la mécanique lagrangienne est beaucoup plus élégante mais nécessite la compréhension de la mécanique lagrangienne bien que les deux approches conduisent finalement à la même solution).

Les deux approches et leurs dérivations formelles sont généralement abordées dans les cours de mathématiques ou de physique du secondaire ou du premier cycle, bien qu'elles puissent être facilement trouvées en utilisant une simple recherche Google ou en visitant ce lien. En observant les équations finales du mouvement, nous remarquons une relation entre quatre quantités:

• L'angle du pendule par rapport à la verticale
• La vitesse angulaire du pendule
• L'accélération angulaire du pendule
• L'accélération linéaire du chariot

Où les trois premières sont des quantités qui vont être mesurées par le capteur et la dernière quantité va être envoyée à l'actionneur pour effectuer.

Étape 3: Théorie du contrôle

La théorie du contrôle est un sous-domaine des mathématiques qui traite du contrôle et de l'exploitation de systèmes dynamiques dans des processus et des machines d'ingénierie. L'objectif est de développer un modèle de contrôle ou une boucle de contrôle pour atteindre généralement la stabilité. Dans notre cas, équilibrez le pendule à l'envers.

Il existe deux principaux types de boucles de régulation: la régulation en boucle ouverte et la régulation en boucle fermée. Lors de la mise en œuvre d'un contrôle en boucle ouverte, l'action de contrôle ou la commande du contrôleur est indépendante de la sortie du système. Un bon exemple de ceci est un four, où la durée pendant laquelle le four reste allumé dépend uniquement de la minuterie.

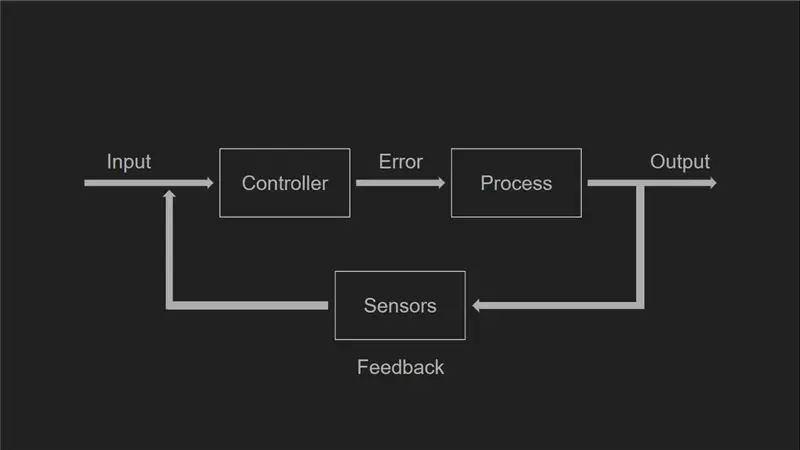
Alors que dans un système en boucle fermée, la commande du contrôleur dépend du retour d'information de l'état du système. Dans notre cas, la rétroaction est l'angle du pendule par rapport à la normale qui détermine la vitesse et la position du chariot, faisant ainsi de ce système un système en boucle fermée. Ci-joint une représentation visuelle sous la forme d'un schéma fonctionnel d'un système en boucle fermée.

Il existe plusieurs techniques de mécanisme de rétroaction, mais l'une des plus utilisées est le contrôleur proportionnel-intégral-dérivé (contrôleur PID), que nous allons utiliser.

Remarque: comprendre le fonctionnement de ces contrôleurs est très utile pour développer un contrôleur réussi, bien qu'expliquer les opérations d'un tel contrôleur dépasse le cadre de cette instruction. Au cas où vous n'auriez pas rencontré ces types de contrôleurs dans votre cours, il existe de nombreux documents en ligne et une simple recherche sur Google ou un cours en ligne vous aidera.

Étape 4: Mettre en œuvre ce projet dans votre classe

Groupe d'âge: Ce projet s'adresse principalement aux étudiants du secondaire ou du premier cycle, mais pourrait également être présenté à des enfants plus jeunes simplement à titre de démonstration en donnant un aperçu des concepts.

Concepts couverts: Les principaux concepts couverts par ce projet sont la dynamique et la théorie du contrôle.

Temps nécessaire: Une fois toutes les pièces rassemblées et fabriquées, l'assemblage prend 10 à 15 minutes. La création du modèle de contrôle nécessite un peu plus de temps, pour cela, les étudiants peuvent disposer de 2 à 3 jours. Une fois que chaque élève (ou groupe d'élèves) a développé ses modèles de contrôle respectifs, une autre journée peut être utilisée pour que les individus ou les équipes fassent la démonstration.

Une façon de mettre en œuvre ce projet dans votre classe serait de construire le système (décrit dans les étapes suivantes), pendant que le lot travaille sur les sous-thèmes de physique liés à la dynamique ou pendant qu'ils étudient les systèmes de contrôle dans les cours de mathématiques. De cette façon, les idées et les concepts rencontrés en cours peuvent être directement mis en œuvre dans une application du monde réel, ce qui rend leurs concepts beaucoup plus clairs, car il n'y a pas de meilleur moyen d'apprendre un nouveau concept que de le mettre en œuvre dans la vie réelle.

Un seul système peut être construit, ensemble en tant que classe, puis la classe peut être divisée en équipes, chacune construisant un modèle de contrôle à partir de zéro. Chaque équipe peut ensuite démontrer son travail dans un format de compétition, où le meilleur modèle de contrôle est celui qui peut équilibrer le plus longtemps et résister aux coups et aux poussées de manière robuste.

Une autre façon de mettre en œuvre ce projet dans votre classe serait de faire en sorte que les enfants plus âgés (niveau secondaire environ), de développer ce projet et de le démontrer aux plus jeunes tout en leur donnant un aperçu de la dynamique et des contrôles. Cela peut non seulement susciter un intérêt pour la physique et les mathématiques chez les plus jeunes, mais aidera également les élèves plus âgés à cristalliser leurs concepts de la théorie, car l'un des meilleurs moyens de renforcer vos concepts est de les expliquer aux autres, en particulier aux plus jeunes, car cela nécessite à vous de formuler vos idées de manière très simple et claire.

Étape 5: Pièces et fournitures

Le chariot pourra se déplacer librement sur un ensemble de rails lui donnant un seul degré de liberté. Voici les pièces et fournitures nécessaires à la fabrication du pendule et du système chariot et rails:

Électronique:

• Une carte compatible Arduino, n'importe laquelle fonctionnera. Je recommande un Uno au cas où vous n'êtes pas trop expérimenté avec l'électronique car ce sera plus simple à suivre.
• Un moteur pas à pas Nema17, qui servira d'actionneur pour le chariot.
• Un pilote de moteur pas à pas, encore une fois tout fonctionnera, mais je recommande le pilote de moteur pas à pas A4988 car il sera juste plus simple à suivre.
• Un MPU-6050 Six-Axis (Gyro + Accéléromètre), qui détectera les différents paramètres tels que l'angle et la vitesse angulaire du pendule.
• Une alimentation 12v 10A, 10A est en fait une légère exagération pour ce projet spécifique, tout ce qui dépasse 3A fonctionnera, mais avoir la possibilité de tirer un courant supplémentaire permet un développement futur où plus de puissance peut être nécessaire.

Matériel:

• 16 x roulements, j'ai utilisé des roulements de skateboard et ils ont très bien fonctionné
• 2 x poulies et courroie GT2
• Environ 2,4 mètres de tuyau en PVC de 1,5 pouce
• Lot d'écrous et boulons de 4 mm

Certaines des pièces qui ont été utilisées dans ce projet ont également été imprimées en 3D, donc avoir une imprimante 3D sera très utile, bien que des installations d'impression 3D locales ou en ligne soient couramment disponibles.

Le coût total de toutes les pièces est juste un peu moins de 50$ (excluant l'imprimante 3D)

Étape 6: Pièces imprimées en 3D

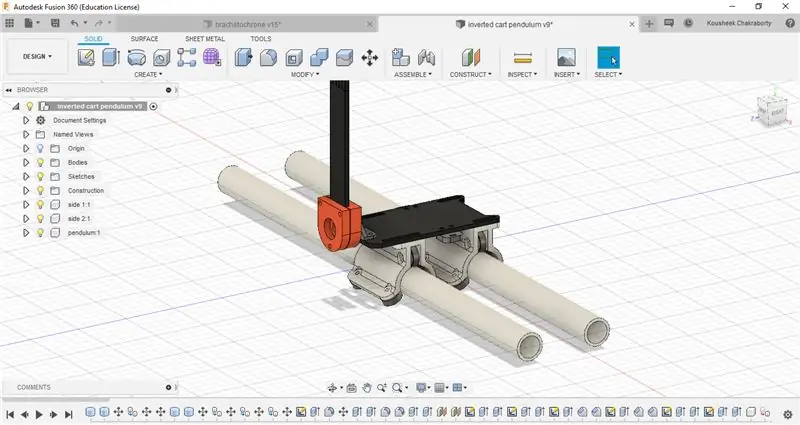
Certaines parties du système de chariot et de rails devaient être fabriquées sur mesure, j'ai donc utilisé gratuitement Fusion360 d'Autodesk pour modéliser les fichiers CAO et les imprimer en 3D sur une imprimante 3D.

Certaines des pièces qui étaient purement des formes 2D, comme le pendule et le lit du portique, ont été découpées au laser car c'était beaucoup plus rapide. Tous les fichiers STL sont joints ci-dessous dans le dossier zippé. Voici une liste complète de toutes les pièces:

• 2 x rouleau de portique
• 4 x embouts
• 1 x support pas à pas
• 2 x support de roulement de poulie de ralenti
• 1 x support de pendule
• 2 x attache de ceinture
• 1 x support de roulement pendulaire (a)
• 1 x support de roulement pendulaire (b)
• 1 x entretoise de trou de poulie
• 4 x entretoise de trou de roulement
• 1 x plaque de portique
• 1 x plaque de support pas à pas
• 1 x plaque de support de poulie de ralenti
• 1 x pendule (a)
• 1 x pendule (b)

Au total, il y a 24 pièces, qui ne prennent pas trop de temps à imprimer car les pièces sont petites et peuvent être imprimées ensemble. Au cours de cette instructable, je ferai référence aux parties basées sur les noms de cette liste.

Étape 7: Assemblage des rouleaux du portique

Les rouleaux du portique sont comme les roues du chariot. Ceux-ci rouleront le long de la piste en PVC, ce qui permettra au chariot de se déplacer en douceur avec un minimum de friction. Pour cette étape, prenez les deux rouleaux de portique imprimés en 3D, 12 roulements et un tas d'écrous et de boulons. Vous aurez besoin de 6 roulements par rouleau. Fixez les roulements au rouleau à l'aide des écrous et des boulons (utilisez les images comme référence). Une fois chaque rouleau réalisé, glissez-les sur le tuyau en PVC.

Étape 8: Assemblage du système d'entraînement (moteur pas à pas)

Le chariot sera entraîné par un moteur pas à pas Nema17 standard. Fixez le moteur dans le support du moteur pas à pas à l'aide des vis qui auraient dû être fournies avec le moteur pas à pas. Vissez ensuite le support sur la plaque de support du moteur pas à pas, alignez les 4 trous du support avec les 4 de la plaque et utilisez des écrous et des boulons pour fixer les deux ensemble. Ensuite, montez la poulie GT2 sur l'arbre du moteur et fixez les 2 embouts à la plaque de support du moteur pas à pas par le bas en utilisant plus d'écrous et de boulons. Une fois cela fait, vous pouvez glisser les embouts sur les tuyaux. Si l'ajustement est trop juste au lieu de forcer les embouts sur les tuyaux, je recommande de poncer la surface intérieure de l'embout imprimé en 3D jusqu'à ce que l'ajustement soit bien ajusté.

Étape 9: Assemblage du système d'entraînement (poulie de ralenti)

Les écrous et boulons que j'utilisais avaient un diamètre de 4 mm bien que les alésages de la poulie et des roulements aient été de 6 mm, c'est pourquoi j'ai dû imprimer des adaptateurs en 3D et les enfoncer dans les trous de la poulie et des roulements pour qu'ils ne le fassent pas. vaciller sur le boulon. Si vous avez des écrous et des boulons de la bonne taille, vous n'aurez pas besoin de cette étape.

Monter les roulements dans le support de roulement de poulie folle. Encore une fois, si l'ajustement est trop serré, utilisez du papier de verre pour poncer légèrement la paroi intérieure du support de roulement de poulie folle. Passez un boulon dans l'un des roulements, puis glissez une poulie sur le boulon et fermez l'autre extrémité avec le deuxième jeu de supports de roulement et de poulie folle.

Une fois cela fait, fixez la paire de supports de roulement de poulie folle sur la plaque de support de poulie folle et fixez les embouts à la face inférieure de cette plaque, comme à l'étape précédente. Enfin, bouchez l'extrémité opposée des deux tuyaux en PVC à l'aide de ces embouts. Avec cela, les rails de votre chariot sont complets.

Étape 10: Assemblage du portique

L'étape suivante consiste à construire le chariot. Fixez les deux rouleaux ensemble à l'aide de la plaque du portique et de 4 écrous et boulons. Les plaques du portique ont des fentes afin que vous puissiez ajuster la position de la plaque pour de légers ajustements.

Ensuite, montez les deux attaches de ceinture des deux côtés de la plaque du portique. Assurez-vous de les attacher par le bas sinon la ceinture ne sera pas au même niveau. Assurez-vous de passer également les boulons par le bas, car sinon, si les boulons sont trop longs, ils peuvent obstruer la courroie.

Enfin, fixez le support du pendule à l'avant du chariot à l'aide d'écrous et de boulons.

Étape 11: Assemblage du pendule

Le pendule a été réalisé en deux pièces simplement pour économiser de la matière. Vous pouvez coller les deux pièces ensemble en alignant les dents et en les supercollant. Poussez à nouveau les entretoises des trous de roulement dans les deux roulements pour compenser les diamètres de boulon plus petits, puis poussez les roulements dans les trous de roulement des deux pièces de support de roulement pendulaire. Fixez les deux pièces imprimées en 3D de chaque côté de l'extrémité inférieure du pendule et fixez les 3 ensemble à l'aide de 3 écrous et boulons passant à travers les supports de roulement du pendule. Passez un boulon à travers les deux roulements et fixez l'autre extrémité avec un écrou correspondant.

Ensuite, saisissez votre MPU6050 et fixez-le à l'extrémité opposée du pendule à l'aide de vis de montage.

Étape 12: Montage du pendule et des courroies

La dernière étape consiste à monter le pendule sur le chariot. Pour ce faire, faites passer le boulon que vous aviez précédemment passé dans les deux roulements du pendule, dans le trou du support de pendule fixé à l'avant du chariot et utilisez un écrou à l'autre extrémité pour fixer le pendule sur le chariot.

Enfin, saisissez votre ceinture GT2 et fixez d'abord une extrémité à l'une des attaches de ceinture qui est fixée sur le chariot. Pour cela, j'ai utilisé un clip de ceinture imprimable en 3D qui se clipse sur l'extrémité de la ceinture et l'empêche de glisser à travers la fente étroite. Les stls de cette pièce peuvent être trouvées sur Thingiverse en utilisant ce lien. Enroulez la courroie tout autour de la poulie pas à pas et de la poulie folle et fixez l'autre extrémité de la courroie à la pièce de fixation de la courroie à l'extrémité opposée du chariot. Tendez la courroie en veillant à ne pas trop serrer ou la laisser trop lâche et avec cela votre pendule et votre chariot sont complets !

Étape 13: Câblage et électronique

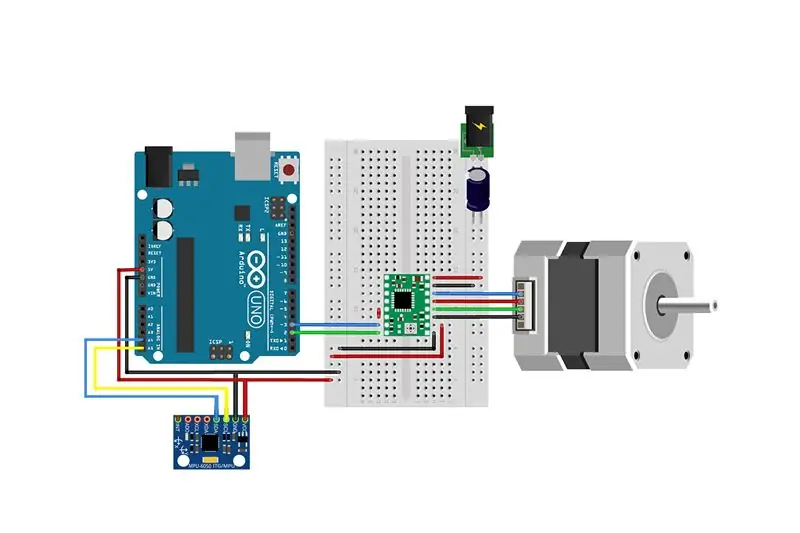
Le câblage consiste à connecter le MPU6050 à l'Arduino et le câblage du système d'entraînement. Suivez le schéma de câblage ci-joint pour connecter chaque composant.

MPU6050 vers Arduino:

• GND à GND
• +5v à +5v
• SDA vers A4
• SCL à A5
• Int à D2

Moteur pas à pas vers pilote pas à pas:

• Bobine 1(a) à 1A
• Bobine 1(b) à 1B
• Bobine 2(a) à 2A
• Bobine 2(b) à 2B

Pilote pas à pas vers Arduino:

• GND à GND
• VDD à +5v
• PAS à D3
• DIR à D2
• VMOT à la borne positive de l'alimentation
• GND à la borne de terre de l'alimentation

Les broches Sleep et Reset sur le pilote pas à pas doivent être connectées avec un cavalier. Et enfin, c'est une bonne idée de connecter un condensateur électrolytique d'environ 100 uF en parallèle avec les bornes positive et de masse de l'alimentation.

Étape 14: Contrôle du système (contrôle proportionnel)

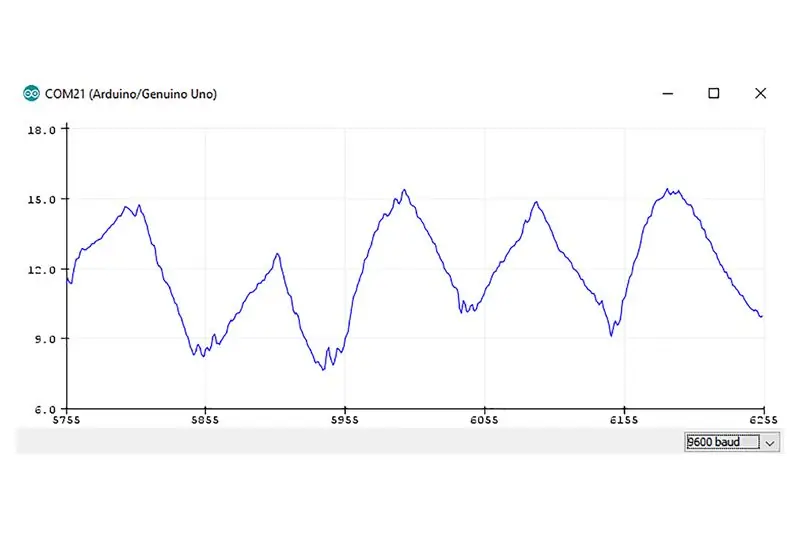
Au départ, j'ai décidé d'essayer un système de contrôle proportionnel de base, c'est-à-dire que la vitesse du chariot est simplement proportionnelle par un certain facteur à l'angle que fait le pendule avec la verticale. Il s'agissait simplement d'un test pour s'assurer que toutes les pièces fonctionnaient correctement. Cependant, ce système proportionnel de base était suffisamment robuste pour que le pendule soit déjà en équilibre. Le pendule pourrait même contrer des poussées douces et des coups de coude assez robustes. Alors que ce système de contrôle fonctionnait remarquablement bien, il avait encore quelques problèmes. Si l'on regarde le graphique des lectures de l'IMU sur un certain temps, nous pouvons clairement remarquer des oscillations dans les lectures des capteurs. Cela implique que chaque fois que le contrôleur essaie de faire une correction, il dépasse toujours d'un certain montant, ce qui est, en fait, la nature même d'un système de contrôle proportionnel. Cette légère erreur peut être corrigée en implémentant un type de contrôleur différent qui prend en compte tous ces facteurs.

Le code du système de contrôle proportionnel est joint ci-dessous. Le code nécessite la prise en charge de quelques bibliothèques supplémentaires qui sont la bibliothèque MPU6050, la bibliothèque PID et la bibliothèque AccelStepper. Ceux-ci peuvent être téléchargés à l'aide du gestionnaire de bibliothèque intégré de l'IDE Arduino. Allez simplement dans Sketch >> Inclure la bibliothèque >> Gérer les bibliothèques, puis recherchez simplement PID, MPU6050 et AccelStepper dans la barre de recherche et installez-les en cliquant simplement sur le bouton Installer.

Cependant, mon conseil à tous ceux d'entre vous qui sont passionnés de sciences et de mathématiques serait d'essayer de créer un contrôleur de ce type à partir de zéro. Cela renforcera non seulement vos concepts sur les théories de la dynamique et des commandes, mais vous donnera également l'occasion de mettre en œuvre vos connaissances dans des applications réelles.

Étape 15: Contrôle du système (contrôle PID)

Généralement, dans la vraie vie, une fois qu'un système de contrôle s'avère suffisamment robuste pour son application, les ingénieurs se contentent généralement de terminer le projet plutôt que de compliquer les situations en utilisant des systèmes de contrôle plus complexes. Mais dans notre cas, nous construisons ce pendule inversé à des fins purement éducatives. Par conséquent, nous pouvons essayer de progresser vers des systèmes de contrôle plus complexes tels que le contrôle PID, qui peuvent s'avérer beaucoup plus robustes qu'un système de contrôle proportionnel de base.

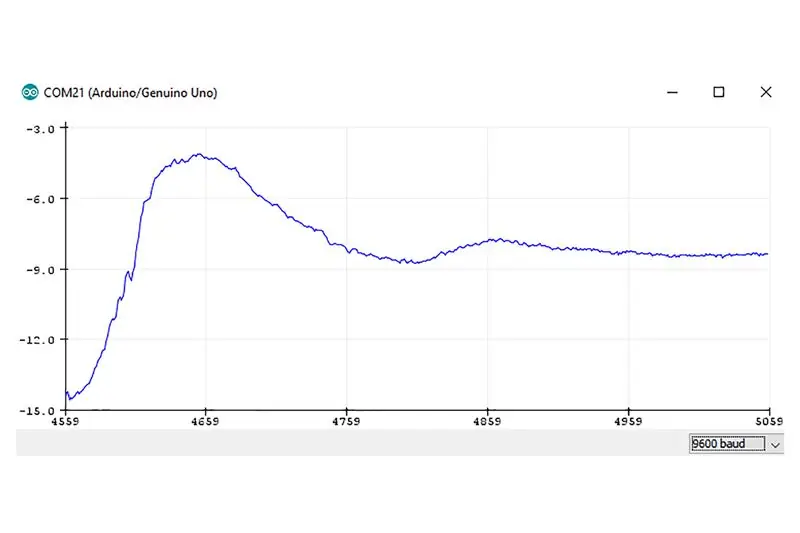
Bien que le contrôle PID soit beaucoup plus complexe à mettre en œuvre, une fois mis en œuvre correctement et en trouvant les paramètres de réglage parfaits, le pendule s'équilibrait nettement mieux. À ce stade, il pourrait également contrer les à-coups légers. Les relevés de l'IMU sur un temps donné (en pièce jointe ci-dessus) prouvent également que les relevés ne s'éloignent jamais trop de la consigne souhaitée, c'est-à-dire la verticale, démontrant que ce système de contrôle est bien plus efficace et robuste que le contrôle proportionnel de base.

Encore une fois, mon conseil à tous ceux d'entre vous qui sont passionnés de sciences et de mathématiques serait d'essayer de créer un contrôleur PID à partir de zéro avant d'utiliser le code joint ci-dessous. Cela peut être considéré comme un défi, et on ne sait jamais, quelqu'un pourrait proposer un système de contrôle bien plus robuste que tout ce qui a été tenté jusqu'à présent. Bien qu'une bibliothèque PID robuste soit déjà disponible pour Arduino, développée par Brett Beauregard, elle peut être installée à partir du gestionnaire de bibliothèque sur l'IDE Arduino.

Remarque: Chaque système de contrôle et ses résultats sont illustrés dans la vidéo jointe à la toute première étape.

Étape 16: autres améliorations

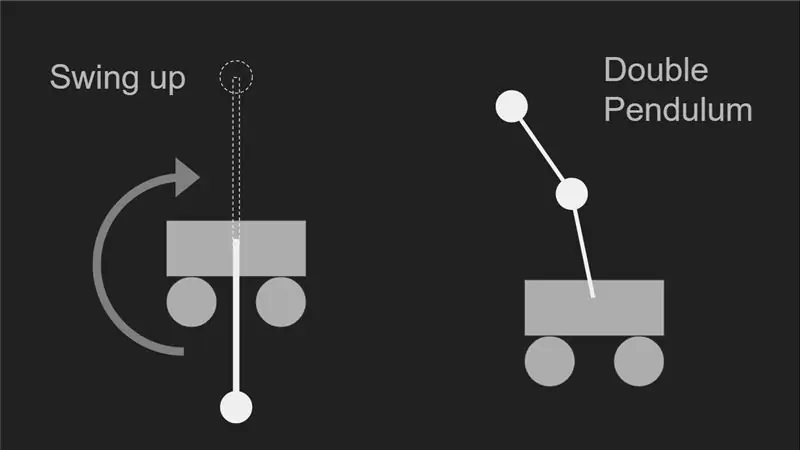
L'une des choses que je voulais essayer était une fonction « swing-up », où le pendule est initialement suspendu sous le chariot et le chariot effectue quelques mouvements rapides de haut en bas le long de la piste pour faire pivoter le pendule d'une suspension position à une position inversée à l'envers. Mais ce n'était pas faisable avec la configuration actuelle car un long câble devait connecter la centrale inertielle à l'Arduino, donc un cercle complet fait par le pendule peut avoir fait tordre et accrocher le câble. Ce problème peut être résolu en utilisant un encodeur rotatif fixé au pivot du pendule au lieu d'une unité de mesure inertielle à l'extrémité de celui-ci. Avec un encodeur, son arbre est la seule chose qui tourne avec le pendule, tandis que le corps reste immobile, ce qui signifie que les câbles ne se tordent pas.

Une deuxième fonctionnalité que je voulais essayer, était d'équilibrer un double pendule sur le chariot. Ce système se compose de deux pendules reliés l'un après l'autre. Bien que la dynamique de tels systèmes soit beaucoup plus complexe et nécessite beaucoup plus de recherches.

Étape 17: Résultats finaux

Une expérience comme celle-ci peut transformer l'ambiance d'une classe de manière positive. Généralement, la plupart des gens préfèrent pouvoir appliquer des concepts et des idées pour les cristalliser, sinon, les idées restent « dans l'air » ce qui fait que les gens ont tendance à les oublier plus rapidement. Ce n'était qu'un exemple d'application de certains concepts appris en classe dans une application réelle, bien que cela suscitera certainement l'enthousiasme des étudiants pour éventuellement essayer de proposer leurs propres expériences pour tester les théories, ce qui rendra leurs futurs cours beaucoup plus vivant, ce qui leur donnera envie d'en savoir plus, ce qui leur fera proposer de nouvelles expériences et ce cycle positif se poursuivra jusqu'à ce que les futures salles de classe soient pleines d'expériences et de projets aussi amusants et agréables.

J'espère que ce sera le début de bien d'autres expériences et projets ! Si vous avez aimé cette instructable et l'avez trouvée utile, veuillez déposer un vote ci-dessous dans le "Concours scientifique en classe" et tous les commentaires ou suggestions sont les bienvenus ! Merci!:)

Finaliste du concours scientifique en classe