
Table des matières:
- Auteur John Day day@howwhatproduce.com.
- Public 2024-01-30 09:09.
- Dernière modifié 2025-01-23 14:46.

Récemment, de nombreux travaux ont été effectués sur l'auto-équilibrage des objets. Le concept d'auto-équilibrage a commencé avec l'équilibrage du pendule inversé. Ce concept s'est également étendu à la conception d'avions. Dans ce projet, nous avons conçu un petit modèle de robot auto-équilibré utilisant l'algorithme PID (proportionnel, intégral, dérivé). Depuis, cette méthode est le nouveau visage des systèmes de contrôle des procédés industriels. Ce rapport passe en revue les méthodes impliquées dans l'auto-équilibrage des objets. Ce projet a été mené comme un projet de semestre pour comprendre la corrélation du PID sur l'efficacité de divers processus industriels. Ici, nous nous concentrons uniquement sur un bref aperçu de l'efficacité et de l'application du contrôle PID. Ce document a été développé en fournissant une brève introduction aux systèmes de contrôle et aux terminologies associées, ainsi qu'aux motivations du projet. Des expérimentations et des observations ont été faites, les mérites et les inconvénients ont été décrits et se terminent par les améliorations futures. Un modèle de robot auto-équilibré a été développé pour comprendre l'ecacité du PID dans le monde du système de contrôle. En passant par des tests et des expériences rigoureux, les avantages et les inconvénients du système de contrôle PID ont été découverts. Il a été constaté qu'en dépit des nombreux avantages du contrôle PID par rapport aux méthodes antérieures, ce système nécessite encore de nombreuses améliorations. On espère que le lecteur comprendra bien l'importance de l'auto-équilibrage, l'efficacité et les insuffisances du contrôle PID.
Étape 1: Présentation
Avec l'avènement de l'informatique et l'industrialisation des procédés, tout au long de l'histoire de l'homme, il y a toujours eu des recherches pour développer des moyens d'affiner les procédés et surtout, pour les contrôler à l'aide de machines de manière autonome. Le but étant de réduire l'implication de l'homme dans ces processus, réduisant ainsi l'erreur dans ces processus. Par conséquent, le domaine de « l'ingénierie des systèmes de contrôle » a été développé. L'ingénierie des systèmes de contrôle peut être définie comme l'utilisation de diverses méthodes pour contrôler le fonctionnement d'un processus ou la maintenance d'un environnement constant et préféré, qu'il soit manuel ou automatique.
Un exemple simple pourrait être de contrôler la température dans une pièce. Le contrôle manuel signifie la présence d'une personne sur un site qui vérifie les conditions présentes (capteur), les compare à la valeur souhaitée (traitement) et prend les mesures appropriées pour obtenir la valeur souhaitée (actionneur). Le problème avec cette méthode est qu'elle n'est pas très fiable car une personne est sujette à l'erreur ou à la négligence dans son travail. En outre, un autre problème est que la vitesse du processus initié par l'actionneur n'est pas toujours uniforme, ce qui signifie que parfois il peut se produire plus rapidement que nécessaire ou parfois il peut être lent. La solution à ce problème consistait à utiliser un microcontrôleur pour contrôler le système. Le microcontrôleur est
programmé pour contrôler le processus, selon des spécifications données, connecté dans un circuit (à discuter plus tard), alimenté la valeur ou les conditions souhaitées et contrôle ainsi le processus pour maintenir la valeur souhaitée. L'avantage de ce procédé est qu'aucune intervention humaine n'est requise dans ce procédé. De plus, la vitesse du processus est uniforme
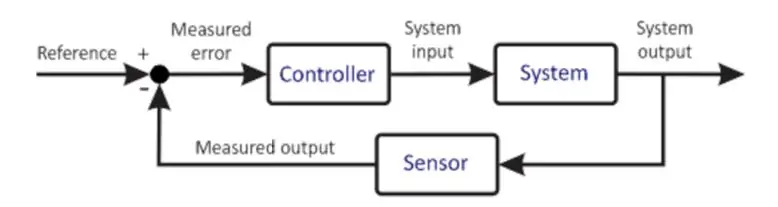
Système de contrôle de base
Le schéma précédent montre une version très simplifiée d'un système de contrôle. Le microcontrôleur est au cœur de tout système de contrôle. C'est un composant très important par conséquent, son choix de sélection doit être fait avec soin en fonction des exigences du système. Le microcontrôleur reçoit une entrée de l'utilisateur. Cette entrée définit l'état souhaité du système. Le microcontrôleur reçoit également une entrée de retour du capteur. Ce capteur est connecté à la sortie du Système, dont les informations sont renvoyées à l'entrée. Le microprocesseur, basé sur sa programmation, effectue divers calculs et fournit une sortie à l'actionneur. L'actionneur, basé sur la sortie, contrôle l'installation pour essayer de maintenir ces conditions. Un exemple pourrait être un pilote de moteur entraînant un moteur où le pilote de moteur est l'actionneur et le moteur est l'usine. Le moteur tourne donc à une vitesse donnée. Le capteur connecté lit l'état de l'installation à l'instant présent et le renvoie au microcontrôleur. Le microcontrôleur compare à nouveau, fait des calculs et ainsi, le cycle se répète. Ce processus est répétitif et sans fin par lequel le microcontrôleur maintient les conditions souhaitées
Étape 2: Système de contrôle basé sur PID
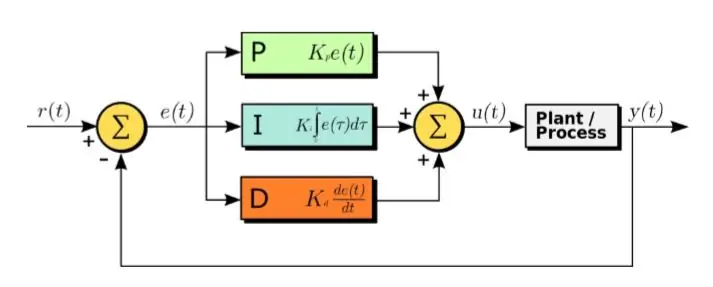

L'algorithme PID est une méthode ecace de conception d'un système de contrôle.
Définition
PID signifie Proportionnel, Intégral et Dérivé. Dans cet algorithme, le signal d'erreur reçu est l'entrée. Et l'équation suivante est appliquée sur le signal d'erreur
U(t) = Kp∗e(t) + Kd∗d/dt(e(t)) + Ki∗intégrale(e(t)) (1.1)
Brève explication
Comme on peut le voir dans l'équation ci-dessus, l'intégrale et la dérivée des signaux d'erreur sont calculées, multipliées par leurs constantes respectives et additionnées avec la constante Kp multipliée par e(t). La sortie est ensuite transmise à l'actionneur qui fait fonctionner le système. Examinons maintenant chaque partie de la fonction à tour de rôle. Cette fonction eecte directement le temps de montée, le temps de descente, le dépassement de crête, le temps de stabilisation et l'erreur en régime permanent.
• Partie proportionnelle: La partie proportionnelle réduit le temps de montée et diminue l'erreur en régime permanent. Cela signifie que le système mettra moins de temps pour atteindre sa valeur de crête et lorsqu'il atteint son état stable, l'erreur d'état stable sera faible. Cependant, cela augmente le dépassement de crête.
• Partie dérivée: La partie dérivée réduit le dépassement et le temps de stabilisation. Cela signifie que l'état transitoire du système sera plus amorti. De plus, le système atteindra son état stable en moins de temps. Cependant, il n'a aucun eet sur le temps de montée ou l'erreur en régime établi.
• Partie intégrale: La partie intégrale réduit le temps de montée et élimine complètement l'erreur de régime permanent. Cependant, il augmente le dépassement de crête et le temps de stabilisation.
• Réglage: un bon système de contrôle aura un temps de montée, un temps de stabilisation, un dépassement de crête et une erreur d'état stable faibles. Par conséquent, les Kp, Kd, Ki doivent être finement réglés pour ajuster la contribution des facteurs ci-dessus afin d'acquérir un bon système de contrôle.
La figure ci-jointe montre l'effet de la modification de divers paramètres dans l'algorithme PID.
Étape 3: Robot auto-équilibrant

Un robot auto-équilibré est un robot multicouche à deux roues.
Le robot essaiera de s'équilibrer lors de l'application de toute force inégale. Il s'équilibrera par application d'une force s'opposant à la résultante des forces sur le robot.
Méthodes d'auto-équilibrage
Il existe quatre méthodes d'auto-équilibrage des robots. Ceux-ci sont les suivants:
Auto-équilibrage à l'aide de deux capteurs d'inclinaison IR
C'est l'un des moyens les plus grossiers d'équilibrer le robot car il nécessite très moins de matériel et un algorithme relativement simple. Dans cette approche, deux capteurs IR inclinés sont utilisés pour mesurer la distance entre le sol et le robot. Sur la base de la distance calculée, le PID peut être utilisé pour entraîner les moteurs afin d'équilibrer le robot en conséquence. Un inconvénient de cette méthode est que le capteur IR peut manquer certaines lectures. Un autre problème est qu'une interruption et des boucles sont nécessaires pour le calcul de la distance, ce qui augmente la complexité temporelle de l'algorithme. Par conséquent, cette méthode d'équilibrage du robot n'est pas très ecace.
Auto-équilibrage à l'aide d'un accéléromètre
L'accéléromètre nous donne l'accélération du corps sur 3 axes. L'accélération orientée dans l'axe y (vers le haut) et l'axe x (vers l'avant) nous donne la mesure pour calculer la direction de la gravité et donc calculer l'angle d'inclinaison. L'angle est calculé comme suit:
θ = arctan(Ay/Ax) (1.2)
L'inconvénient d'utiliser cette méthode est que pendant le mouvement du robot, l'accélération horizontale sera également ajoutée aux lectures qui est un bruit à haute fréquence. Par conséquent, l'angle d'inclinaison sera inexact.
Auto-équilibrage à l'aide du gyroscope
Un gyroscope est utilisé pour calculer les vitesses angulaires le long des trois axes. L'angle d'inclinaison est obtenu à l'aide de l'équation suivante.
p(i) = θp(i−1) + 1/6(vali−3 + 2vali−2 + 2vali−1 + vali) (1.3)
Un gros inconvénient de l'utilisation du gyroscope est qu'il a un petit DC Bias qui est un bruit à basse fréquence et dans quelques temps les valeurs renvoyées sont complètement fausses. Ceci, après intégration, fera dériver le point zéro. De ce fait, le robot restera dans sa position verticale pendant un certain temps et se renversera une fois la dérive venue.
Auto-équilibrage utilisant à la fois l'accéléromètre et le gyroscope
Comme indiqué ci-dessus, l'utilisation uniquement d'un accéléromètre ou d'un gyroscope ne nous donnera pas le bon angle d'inclinaison. Pour tenir compte de cela, l'accéléromètre et le gyroscope sont utilisés. Ceux-ci sont tous deux intégrés au MPU6050. Dans ce cas, nous obtenons les données des deux, puis les fusionnons en utilisant soit le filtre de Kalman, soit le filtre complémentaire.
• Filtre de Kalman: le filtre de Kalman calcule la meilleure estimation de l'état d'un système dynamique à partir de mesures bruitées, minimisant l'erreur quadratique moyenne de l'estimation. Il fonctionne en deux étapes, prédiction et correction, compte tenu des équations stochastiques discrètes décrivant la dynamique du système. Cependant, il s'agit d'un algorithme très complexe à implémenter surtout sur un matériel limité d'un microcontrôleur.
• Filtre complémentaire: Cet algorithme utilise principalement les données obtenues du gyroscope et les intègre au fil du temps pour obtenir l'angle d'inclinaison. Il utilise également une petite proportion des lectures de l'accéléromètre. Le filtre complémentaire, en fait, minimise le bruit à haute fréquence de l'accéléromètre et le bruit à basse fréquence du gyroscope, puis les fusionne pour donner le meilleur angle d'inclinaison précis.
Étape 4: Conception du robot
Nous avons conçu un robot auto-équilibré utilisant un contrôleur proportionnel dérivé implémenté par Complementary Filter pour MPU6050. Ce petit modèle d'Auto Balancing Robot nous illustrera l'utilité des Systèmes de Contrôle dans l'Auto Balancing des robots.
Mise en place du système:
Le système est un robot auto-équilibré. Il est implémenté à l'aide du contrôleur PID qui est un contrôleur dérivé intégral proportionnel. On équilibre le robot en entraînant ses roues dans le sens de sa chute. Ce faisant, nous essayons de maintenir le centre de gravité du robot au-dessus du point de pivot. Pour entraîner les roues dans le sens de sa chute, il faut savoir où tombe le robot et à quelle vitesse il tombe. Ces données sont obtenues à l'aide du MPU6050 qui possède un accéléromètre et un gyroscope. Le MPU6050 mesure l'angle d'inclinaison et donne sa sortie au micro-contrôleur. Le MPU6050 est interfacé avec la carte STM via I2C. Dans I2C, un fil est pour l'horloge qui s'appelle SCL. L'autre est pour le transfert de données qui est SDA. Dans ce cas, la communication maître-esclave est utilisée. L'adresse de début et l'adresse de fin sont spécifiées pour savoir d'où les données commencent et où elles se terminent. Nous avons implémenté le filtre complémentaire ici pour MPU6050 qui est un filtre mathématique pour fusionner les sorties de l'accéléromètre et du gyroscope. Après avoir obtenu les données du MPU6050, le microcontrôleur effectuera des calculs pour savoir où il tombe. Sur la base des calculs, le microcontrôleur STM donnera des commandes au conducteur du moteur pour conduire les véhicules dans le sens de la chute, ce qui équilibrera le robot.
Étape 5: Composants du projet



Les composants suivants ont été utilisés dans le projet de robot à équilibrage automatique:
STM32F407
Un microcontrôleur conçu par ST Microelectronics. Il fonctionne sur l'architecture ARM Cortex-M.
Pilote de moteur L298N
Ce circuit intégré est utilisé pour faire fonctionner le moteur. Il reçoit deux entrées externes. Celui du microcontrôleur qui lui fournit un signal PWM. En ajustant la largeur de l'impulsion, la vitesse du moteur peut être ajustée. Sa deuxième entrée est la source de tension nécessaire pour entraîner le moteur qui est une batterie 12V dans notre cas.
Moteur à courant continu
Un moteur à courant continu fonctionne sur une alimentation en courant continu. Dans cette expérience, le moteur à courant continu fonctionne à l'aide des optocoupleurs connectés au pilote du moteur. Pour entraîner le moteur, nous avons utilisé le Motor Drive L298N.
MPU6050
Le MPU6050 est utilisé pour obtenir des informations sur l'endroit où le robot tombe. Il mesure l'angle d'inclinaison par rapport au point d'inclinaison zéro qui est la position du MPU6050 lorsque le programme démarre.
Le MPU6050 possède un accéléromètre 3 axes et un gyroscope 3 axes. L'accéléromètre mesure l'accélération le long des trois axes et le gyroscope mesure la vitesse angulaire autour des trois axes. Afin de combiner la sortie, nous devons filtrer les bruits des deux. Pour filtrer les bruits, nous avons le filtre de Kalman et complémentaire. Nous avons mis en place un filtre complémentaire dans notre projet.
Opto Couple 4N35
Un optocoupleur est un dispositif utilisé pour isoler la partie basse tension et la partie haute tension du circuit. Comme son nom l'indique, il fonctionne sur la base de la lumière. Lorsque la partie basse tension reçoit un signal, le courant circule dans la partie haute tension
Étape 6: Structure du robot
La structure du robot est expliquée comme suit:
Structure physique
Le robot auto-équilibré se compose de deux couches constituées de verre plastique transparent. Les détails de deux couches sont donnés ci-dessous:
Première couche
Dans la partie inférieure de la première couche, nous avons placé une cellule pour alimenter la carte STM. De plus, deux moteurs de 4 volts chacun ont été placés de chaque côté avec des pneus connectés pour que le robot se déplace. Dans la partie supérieure de la première couche, deux batteries de 4 volts chacune (8 volts au total) et un circuit de commande de moteur (L298N) ont été placés pour le fonctionnement des moteurs.
Deuxième couche
Dans la couche supérieure du robot, nous avons placé le STM Board sur Perf Board. Une autre planche perforée de 4 coupleurs opto est placée sur la couche supérieure. Le gyroscope est également placé sur la couche supérieure du robot depuis le côté inférieur. Les deux composants sont placés dans la partie centrale de sorte que le centre de gravité soit maintenu aussi bas que possible.
Centre de gravité du robot
Le centre de gravité est maintenu aussi bas que possible. À cette fin, nous avons placé des batteries lourdes sur la couche inférieure et des composants légers tels que la carte STM et les optocoupleurs sur la couche supérieure.
Étape 7: Coder
Le code a été compilé sur Atollic TrueStudio. Le studio STM a été utilisé à des fins de débogage.
Étape 8: Conclusion
Après beaucoup d'expérimentations et d'observations, nous arrivons enfin au point où nous résumons nos résultats et discutons dans quelle mesure nous avons réussi à mettre en œuvre et à déterminer l'efficacité du système.
Revue générale
Au cours de l'expérimentation, la vitesse du moteur a été contrôlée avec succès à l'aide de l'algorithme PID. La courbe n'est cependant pas exactement une ligne droite lisse. Il y a plusieurs raisons à cela:
• Le capteur bien que connecté à un filtre passe-bas assure encore certains anti-rebonds finis; ceux-ci sont dus aux résistances non linéaires et à certaines raisons inévitables de l'électronique analogique.
• Le moteur ne tourne pas régulièrement sous une faible tension ou PWM. Il fournit des à-coups qui peuvent provoquer des valeurs erronées transmises au système.
• En raison de l'oscillation, le capteur peut manquer certaines fentes fournissant des valeurs plus élevées. • Une autre cause majeure d'erreur peut être la fréquence d'horloge centrale du microcontrôleur STM. Ce modèle de microcontrôleur STM fournit une horloge centrale de 168 MHz. Bien que ce problème soit traité dans ce projet, il existe une notion globale à propos de ce modèle selon laquelle il ne fournit pas exactement une fréquence aussi élevée.
La vitesse en boucle ouverte fournit une ligne très lisse avec seulement quelques valeurs inattendues. L'algorithme PID fonctionne également très bien, fournissant un temps de stabilisation très faible du moteur. L'algorithme PID du moteur a été testé sous différentes tensions en maintenant la vitesse de référence constante. Le changement de tension ne change pas la vitesse du moteur montrant que l'algorithme PID fonctionne correctement
Efficacité
Nous discutons ici de l'ecacité du contrôleur PID que nous avons observé au cours de l'expérimentation.
Mise en œuvre simple
Nous avons vu dans la partie expérimentation et observations qu'un régulateur PID est très simple à mettre en œuvre. Il ne nécessite que trois paramètres ou constantes qui doivent être réglés afin d'avoir un système de contrôle de vitesse
Efficacité inégalée pour les systèmes linéaires
Le contrôleur PID linéaire est le plus efficace de la famille des contrôleurs car la logique est très simple et l'application est répandue dans le cas d'applications linéaires ou assez linéaires.
Limites
Nous avons expliqué dans l'abstrait les limites de ce système. Nous discutons ici de quelques-uns d'entre eux que nous avons observés.
Sélection de constantes
Nous avons vu que, bien qu'un contrôleur PID soit facile à mettre en œuvre, il reste un inconvénient majeur du système que l'étape de sélection de la valeur des constantes soit laborieuse; car il faut faire des calculs diciles. L'autre méthode est la méthode hit and trial, mais elle n'est pas non plus ecace.
Constantes pas toujours constantes
Les résultats expérimentaux ont montré que pour différentes valeurs de la vitesse de référence du moteur, le contrôleur PID fonctionnait mal pour les mêmes valeurs des constantes PID. Pour des vitesses différentes, les constantes devaient être sélectionnées différemment, ce qui augmente le coût de calcul de façon exponentielle.
Non linéaire
Le contrôleur PID utilisé dans notre cas est linéaire, par conséquent, il ne peut être appliqué qu'aux systèmes linéaires. Pour les systèmes non linéaires, le contrôleur doit être implémenté différemment. Bien que différentes méthodes non linéaires de PID soient disponibles, elles nécessitent la sélection de plus de paramètres. Cela rend à nouveau le système indésirable en raison du coût de calcul élevé.
Poussée initiale requise
Nous avons montré dans la partie expérimentation que pour une vitesse de référence assez faible où l'erreur est assez faible au démarrage, le PWM fourni par le PID est si faible qu'il ne génère pas le couple de démarrage requis pour le moteur. Ainsi, le moteur dans certains essais ne fonctionne pas ou dans d'autres essais fournit un grand dépassement et un temps de stabilisation plus long.
Étape 9: Remerciements spéciaux
Remerciements particuliers aux membres de mon groupe qui m'ont aidé dans ce projet.
Je mettrai bientôt le lien vers la vidéo.
J'espère que vous trouverez cette instructable intéressante.
Voici Tahir Ul Haq de l'UET qui signe. À votre santé !!!
Conseillé:
Robot auto-équilibrant - Algorithme de contrôle PID : 3 étapes

Robot à équilibrage automatique - Algorithme de contrôle PID : Ce projet a été conçu parce que je souhaitais en savoir plus sur les algorithmes de contrôle et sur la manière de mettre en œuvre efficacement des boucles PID fonctionnelles. Le projet est encore en phase de développement car un module Bluetooth n'a pas encore été ajouté qui sera al
Algorithme Cordic utilisant VHDL : 4 étapes
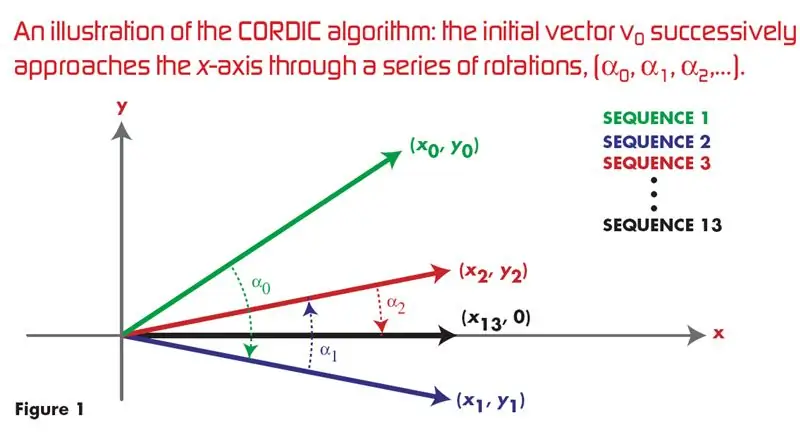
Cordic Algorithm Using VHDL : ## Ceci est le lien le plus cliqué et le plus populaire de Google pour l'implémentation VHDL de l'ALGORITHME CORDIC pour générer des ondes sinus et cosinus## À l'heure actuelle, de nombreux algorithmes efficaces pour le matériel existent, mais ils ne sont pas bien connus en raison de la domination du logiciel
Plateforme Stewart à équilibrage de balle contrôlé par PID : 6 étapes

PID Controlled Ball Balancing Stewart Platform : Motivation et concept général : En tant que physicien en formation, je suis naturellement attiré par les systèmes physiques et je cherche à les comprendre. J'ai été formé pour résoudre des problèmes complexes en les décomposant en leurs ingrédients les plus basiques et essentiels, puis
Création d'un robot à équilibrage automatique Arduino contrôlé à distance : B-robot EVO : 8 étapes

Création d'un robot à équilibrage automatique Arduino contrôlé à distance : B-robot EVO : ------------------------------------ --------------MISE À JOUR : il existe une nouvelle version améliorée de ce robot ici : Le B-robot EVO, avec de nouvelles fonctionnalités !------------ --------------------------------------Comment ça marche ?B-ROBOT EVO est un contrôler
Contrôle de la vitesse du moteur à courant continu à l'aide de l'algorithme PID (STM32F4) : 8 étapes (avec images)

Contrôle de la vitesse du moteur à courant continu à l'aide de l'algorithme PID (STM32F4) : bonjour à tous, voici tahir ul haq avec un autre projet. Cette fois, c'est STM32F407 en tant que MC. Il s'agit d'un projet de fin de semestre. J'espère que vous l'aimez. Cela nécessite beaucoup de concepts et de théorie, alors nous y allons d'abord. Avec l'avènement des ordinateurs et de la
