
Table des matières:
- Auteur John Day day@howwhatproduce.com.
- Public 2024-01-30 09:09.
- Dernière modifié 2025-01-23 14:46.

Salut! Pour satisfaire mon intérêt pour la programmation et, espérons-le, aider à satisfaire le vôtre, je voudrais vous montrer une visionneuse 3D que j'ai codée en javascript. Si vous souhaitez approfondir votre compréhension des jeux 3D ou même créer votre propre jeu 3D, ce prototype de visionneuse 3D est parfait pour vous.
Étape 1: La théorie

Pour comprendre la théorie de cette visionneuse 3D, vous pouvez simplement examiner la façon dont vous visualisez votre environnement (cela permet de n'avoir qu'une seule source de lumière significative). Remarquerez que:
- Les objets plus éloignés de vous occupent une plus petite partie de votre champ de vision.
- Les objets plus éloignés de la source lumineuse apparaissent de couleur plus foncée.
- Au fur et à mesure que les surfaces deviennent plus parallèles (moins perpendiculaires) à la source lumineuse, elles apparaissent de couleur plus foncée.
J'ai décidé de représenter un champ de vision avec un tas de lignes provenant d'un seul point (analogue au globe oculaire). Comme une boule à crampons, les lignes doivent être régulièrement espacées pour s'assurer que chaque partie du champ de vision est représentée de manière égale. Dans l'image ci-dessus, remarquez comment les lignes provenant de la balle à crampons deviennent plus espacées à mesure qu'elles s'éloignent du centre de la balle. Cela permet de visualiser la mise en œuvre du programme de l'observation 1 puisque la densité des lignes diminue à mesure que les objets s'éloignent du point central.
Les lignes sont l'unité de vision de base dans le programme, et elles sont chacune mappées à un pixel sur l'écran. Lorsqu'une ligne croise un objet, son pixel correspondant est coloré en fonction de sa distance par rapport à la source lumineuse et de son angle par rapport à la source lumineuse.
Étape 2: Théorie de la mise en œuvre

Pour simplifier le programme, la source lumineuse est la même que le point central (globe oculaire: point à partir duquel la carte est vue et d'où proviennent les lignes). Similaire à la tenue d'une lumière juste à côté de votre visage, cela élimine les ombres et permet de calculer beaucoup plus facilement la luminosité de chaque pixel.
Le programme utilise également des coordonnées sphériques, avec le point central de vision à l'origine. Cela permet de générer facilement les lignes (chacune avec un unique thêta: angle horizontal et phi: angle vertical), et fournit la base des calculs. Les lignes avec le même thêta sont mappées sur les pixels de la même ligne. Le phis des angles correspondants augmente sur chaque rangée de pixels.
Pour simplifier les calculs, la carte 3D est composée de plans avec une variable commune (commune x, y ou z), tandis que les deux autres variables non communes sont confinées dans une plage, complétant la définition de chaque plan.
Pour regarder autour de vous avec la souris, les équations du programme prennent en compte une rotation verticale et horizontale lors de la conversion entre les systèmes de coordonnées sphériques et xyz. Ceci a pour effet de préformer une rotation sur l'ensemble des lignes de vision "spike ball".
Étape 3: Mathématiques
Les équations suivantes permettent au programme de déterminer quelles lignes croisent chaque objet et des informations sur chaque intersection. J'ai dérivé ces équations des équations de coordonnées sphériques de base et des équations de rotation 2D:
r=distance, t=thêta(angle horizontal), p=phi(angle vertical), A=rotation autour de l'axe Y(rotation verticale), B=rotation autour de l'axe Z(rotation horizontale)
Kx=(sin(p)*cos(t)*cos(A)+cos(p)*sin(A))*cos(B)-sin(p)*sin(t)*sin(B)
Ky=(sin(p)*cos(t)*cos(A)+cos(p)*sin(A))*sin(B)+sin(p)*sin(t)*cos(B)
Kz=-sin(p)*cos(t)*sin(A)+cos(p)*cos(A)
x=r*Kx
y=r*Ky
z=r*Kz
r^2=x^2+y^2+z^2
éclairage=Klight/r*(Kx ou Ky ou Kz)
p=arccos((x*sin(A)*cos(B)+y*sin(A)*sin(B)+z*cos(A))/r)
t=arccos((x*cos(B)+y*sin(B)-p*sin(A)*cos(p))/(r*cos(A)*sin(p)))
Étape 4: programmer

J'espère que ce prototype de visionneuse 3D vous a aidé à comprendre le fonctionnement des réalités virtuelles 3D. Avec un peu plus de perfectionnement et de codage, cette visionneuse a certainement le potentiel d'être utilisée dans le développement de jeux 3D.
Conseillé:
VISIONNEUSE DE STATUT ESP32 COVID19 : 4 étapes

ESP32 COVID19 STATUS VIEWER: Ce projet obtient simplement le statut de COCID19 au format json et l'affiche dans l'OLED
Visionneuse et convertisseur de négatifs de film : 8 étapes (avec images)

Visionneuse et convertisseur de négatifs de film : j'ai immédiatement ressenti le besoin de pouvoir visualiser et enregistrer rapidement d'anciens négatifs de films. J'en avais plusieurs centaines à trier… Je reconnais qu'il existe différentes applications pour mon smartphone mais je n'ai pas pu obtenir de résultats satisfaisants, c'est donc ce que j'ai fait
Moniteur bébé Arduino avec visionneuse Java : 8 étapes (avec photos)
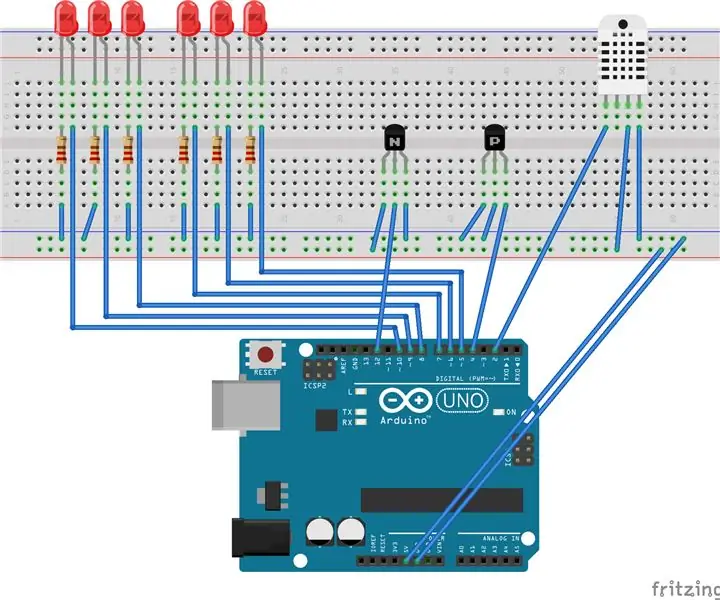
Moniteur bébé Arduino avec visionneuse Java : construisez une unité multi-capteurs basée sur Arduino pour observer les conditions dans une pièce. Cet appareil peut détecter l'humidité, la température, le mouvement et le son. Ci-joint une visionneuse basée sur Java qui reçoit des données série de l'arduino
Visionneuse de webcam tête haute : 7 étapes

Headup Web Cam Viewer : une entrée récente a examiné un système commercial permettant aux utilisateurs de regarder directement leur webcam tout en étant capable de voir la personne à qui ils parlent - style téléprompteur - c'est mon point de vue sur cette idée. Il est facile à construire étant essentiel
Visionneuse de rayons X sur écran d'ordinateur : 4 étapes
Visionneuse de rayons X sur écran d'ordinateur : il s'agit d'une méthode simple pour utiliser votre ordinateur comme une boîte à lumière pour visualiser les rayons X. Briser vos os vient d'atteindre de nouveaux niveaux de plaisir
