
Table des matières:
- Auteur John Day day@howwhatproduce.com.
- Public 2024-01-30 09:05.
- Dernière modifié 2025-01-23 14:45.


Voici une application pratique d'équations mathématiques complexes.
C'est en effet une technique très utile que vous pouvez utiliser pour caractériser des composants, voire une antenne, à des fréquences prédéterminées.
Si vous avez bricolé avec l'électronique, vous connaissez peut-être les résistances et la loi d'Ohm. R = V / I Vous serez peut-être maintenant surpris de savoir que c'est aussi tout ce que vous devez résoudre pour les impédances complexes ! Toutes les impédances sont essentiellement complexes, c'est-à-dire qu'elles ont une partie Réelle et une partie Imaginaire. Dans le cas d'une résistance, l'imaginaire (ou la réactance) est égal à 0, il n'y a donc pas de différence de phase entre V et I, nous pouvons donc les omettre.
Un bref résumé sur les nombres complexes. Complexe signifie simplement que le nombre est composé de deux parties, une réelle et une imaginaire. Il existe deux façons de représenter des nombres complexes, par exemple dans la figure ci-dessus, un point pourrait être défini par les valeurs Réel et Imaginaire, comme l'endroit où les lignes jaune et bleue se rencontrent. Par exemple si la ligne bleue était à 4 sur l'axe X, et 3 sur l'axe Y, ce nombre serait 4 + 3i, i indique que c'est la partie imaginaire de ce nombre. Une autre façon de définir le même point serait la longueur (ou l'amplitude) de la ligne rouge ainsi que l'angle qu'elle fait avec l'horizontale. Dans l'exemple ci-dessus, ce serait 5 < 36,87.
Ou une ligne d'une longueur de 5 à un angle de 36,87 degrés.
Dans l'équation ci-dessus tous les paramètres, R, V et I peuvent être considérés comme ayant une partie imaginaire, lorsque vous travaillez avec des résistances, cette valeur est 0.
Lorsque vous travaillez avec des inductances ou des condensateurs, ou lorsqu'une différence de phase peut être mesurée (en degrés) entre des signaux, l'équation reste la même mais la partie imaginaire du nombre doit être incluse. La plupart des calculatrices scientifiques rendent le travail avec des mathématiques complexes très facile, dans ce tutoriel, je vais travailler à travers un exemple sur un Casio fx-9750GII.
Tout d'abord, un récapitulatif sur l'équation du diviseur de tension de résistance.
Selon la figure -
La tension en Y est le courant i multiplié par R2
i est la tension X divisée par la somme de R1 et R2
Lorsque R2 est inconnu, nous pouvons mesurer les autres valeurs, X, Y, R1 et réarranger l'équation pour résoudre R2.
Fournitures
Calculatrice scientifique
Générateur de signal
Oscilloscope
Étape 1: configuration

Supposons que nous voulons calculer l'inductance du dispositif sous test (DUT) à 1 MHz.
Le générateur de signal est configuré pour une sortie sinusoïdale de 5V à 1MHZ.
Nous utilisons des résistances de 2k ohms et les canaux de l'oscilloscope sont CH1 et CH2
Étape 2: Oscilloscope

Nous obtenons les formes d'onde comme indiqué sur la figure. Un déphasage peut être vu et mesuré sur l'oscilloscope en avance de 130ns. L'amplitude est de 3,4V. Notez que le signal sur CH1 doit être de 2,5 V car il est pris à la sortie du diviseur de tension, ici il est représenté par 5 V pour plus de clarté, car c'est la valeur que nous devons également utiliser dans nos calculs. c'est-à-dire que 5V est la tension d'entrée du diviseur avec la composante inconnue.
Étape 3: Calculer la phase

A 1MHz, la période du signal d'entrée est de 1us.
130ns donne un rapport de 0,13. Ou 13%. 13% de 360 est 46,6
Le signal 5V reçoit un angle de 0.. car il s'agit de notre signal d'entrée et le déphasage lui est relatif.
le signal 3,4V reçoit l'angle de +46,6 (le + signifie qu'il est en avance, pour un condensateur l'angle serait négatif).
Étape 4: Sur la calculatrice


Maintenant, nous entrons simplement nos valeurs mesurées dans la calculatrice.
R est 2k
V est 5 (EDIT - V est 5, plus tard dans l'équation est utilisé X! le résultat est exactement le même que j'ai X comme 5 dans ma calculatrice)
Y est notre tension mesurée avec l'angle de phase, ce nombre est entré comme un nombre complexe, simplement en spécifiant l'angle comme indiqué sur l'écran de la calculatrice
Étape 5: Résoudre l'équation

maintenant l'équation
(Y * R) / (X - Y)
est tapé dans la calculatrice, c'est exactement la même équation que nous utilisons pour résoudre les diviseurs de tension de résistance:)
Étape 6: Valeurs calculées


Le calculateur a donné le résultat
18 + 1872i
Le 18, est la partie réelle de l'impédance et il a une inductance de +1872 à 1MHz.
Ce qui équivaut à 298uH selon l'équation d'impédance de l'inducteur.
18 ohms est supérieur à la résistance qui serait mesurée avec un multimètre, c'est parce que le multimètre mesure la résistance en courant continu. À 1 MHz, il y a un effet de peau, dans lequel la partie interne du conducteur est contournée par le courant et ne circule qu'à l'extérieur du cuivre, diminuant efficacement la surface transversale du conducteur et augmentant sa résistance.
Conseillé:
Comment obtenir n'importe quelle résistance/capacité à l'aide des composants que vous possédez déjà ! : 6 étapes

Comment obtenir n'importe quelle résistance/capacité à l'aide des composants que vous possédez déjà ! : Ce n'est pas simplement un autre calculateur de résistance équivalent série/parallèle ! Ce programme calcule comment combiner les résistances/condensateurs dont vous disposez actuellement pour atteindre une valeur cible de résistance/capacité dont vous avez besoin. Avez-vous déjà eu besoin d'une spécification
Dessouder des composants complexes : 4 étapes

Dessouder des composants complexes : avez-vous déjà voulu retirer cette puce ou ce composant aléatoire de cette carte de circuit imprimé aléatoire que vous avez ? … Et quand les choses se compliquent
Générer des sons de différents types à l'aide d'équations mathématiques (MathsMusic) Arduino : 5 étapes

Génération de sons de différentes sortes à l'aide d'équations mathématiques (MathsMusic) Arduino : Description du projet : Un nouveau voyage a commencé où les idées peuvent être facilement mises en œuvre à l'aide de la communauté open source (Merci à Arduino). Voici donc un moyen · Regardez autour de vous et observez votre environnement · Découvrez les problèmes qui doivent être
Mesurer l'impédance à l'aide de LTspice : 4 étapes
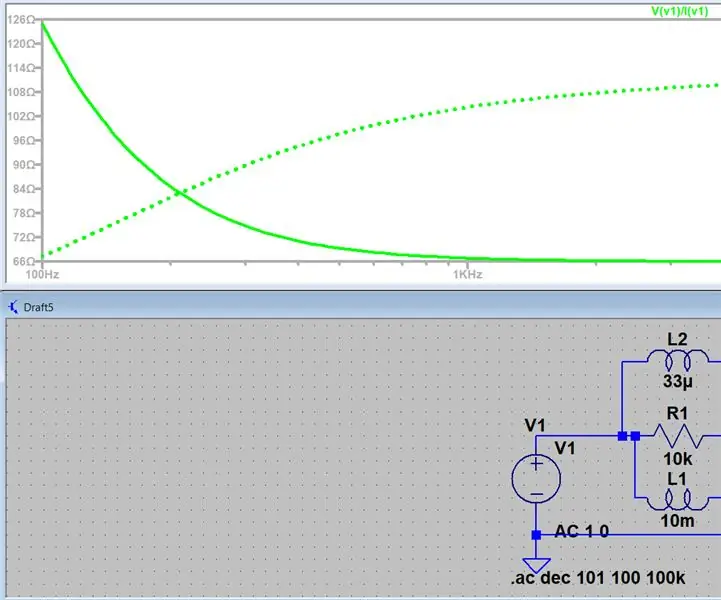
Mesurer l'impédance à l'aide de LTspice : Hé tout le monde, cela va être une introduction simple à la génération d'un balayage CA d'un circuit et à la recherche de l'impédance à un moment donné, cela est revenu plusieurs fois dans mes cours et il m'a été très difficile d'en trouver façon de le faire en ligne donc
Mathématiques rapides 2018 : 7 étapes
Quick Math 2018 : un jeu qui rend l'apprentissage amusant à nouveau
