Observer la prescription de votre globe oculaire : un projet BME60B : 9 étapes

2024 Auteur: John Day | [email protected]. Dernière modifié: 2024-01-30 09:05

Par: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Le grossissement est l'une des caractéristiques clés présentes pour les lunettes de lecture, qui sont classées par leur prescription de dioptries. Selon la Michigan Technology University, une dioptrie est une distance focale de l'objectif, généralement mesurée en mm, en mètres (Michigan Technology University). Étant donné que les lunettes de lecture ont des lentilles convexes, la distance focale serait positive, ce qui entraînerait également des dioptries positives (HyperPhysique). La distance focale augmente à mesure que la distance entre l'objet s'éloigne de l'objectif réel, ce qui entraîne une diminution des dioptries car elles sont inversement proportionnelles. Par conséquent, le fait d'avoir des lunettes de lecture avec des dioptries supplémentaires aiderait l'objectif à zoomer dans la vue de sorte qu'il puisse sembler que la distance focale est inférieure en augmentant la valeur des dioptries.

Le code présenté sera utilisé pour prédire la dioptrie d'un verre à prescription inconnue. Deux entrées sont utilisées pour calculer la prescription: une photographie du fond contrôlé sans utiliser d'objectif, et une autre photographie du même fond mais à travers l'objectif de son choix. Le programme mesurera la distorsion entre ces deux photographies. À partir de là, nous pourrons estimer la dioptrie de l'objectif et produire un résultat que l'utilisateur pourra visualiser.

Pour ce Instructable, vous aurez besoin de:

• Un motif en damier noir et blanc imprimé sur une feuille de papier de 11 x 8,5 pouces
• Un appareil photo avec la possibilité de verrouiller sa mise au point
• Un trépied ou quelque chose de similaire pour sécuriser l'appareil photo
• Diverses prescriptions de lunettes de lecture
• MATLAB

Étape 1: prendre des photos

Afin de calculer le grossissement d'un objectif, vous devez pouvoir le comparer à la taille réelle de l'objet. Pour ce projet, nous comparerons une image agrandie à une image de contrôle.

Ainsi, la première étape consiste à prendre deux photos de la même image - la première à travers l'appareil photo uniquement, et la seconde à travers l'objectif des lunettes de lecture que vous souhaitez tester.

Vous allez prendre une photo d'un damier noir et blanc de 8,5 x 11 pouces avec une grille de 1 pouce. Installez votre caméra à 11 pouces du damier. Avant de prendre les photos, verrouillez la mise au point sur le damier.

Prenez une photo du damier sans les lunettes de lecture. Ensuite, sans rien bouger, placez les lunettes de lecture devant l'appareil photo et prenez la deuxième photo.

Assurez-vous que la position de votre appareil photo ne bouge pas entre les prises de vue. La seule chose qui devrait changer entre les deux photos est la présence de l'objectif des lunettes devant l'appareil photo.

Lorsque vous avez terminé avec les photos, téléchargez-les sur votre ordinateur.

Étape 2: Chargez les images dans MATLAB

Ouvrez un nouveau script.

Tout d'abord, spécifiez le répertoire dans lequel les photos sont stockées. Ensuite, utilisez la fonction dir pour extraire les images-j.webp

Dir = 'C:\Users\kuras\Desktop\classes\SQ2\BME60b\Sandbox\testphotos'; GetDir = dir('*.jpg');

Pour notre projet, nous voulions demander à l'utilisateur du programme pour quels fichiers il voulait comparer. La première section demande à l'utilisateur de spécifier l'image de contrôle, et la seconde demande à l'utilisateur de spécifier l'image de test.

• %Demander à l'utilisateur quel fichier est l'image de contrôle.
• Control = input('# d'image de contrôle.\n');
• ControlFile = [GetDir(Control).name]
• %Demandez à l'utilisateur quel fichier est l'image qu'il souhaite analyser.
• ChooseFile = input('\n# d'image que vous souhaitez analyser.\n');
• PrescripFile = [GetDir(ChooseFile).name];

Étape 3: Analyse d'images

Une image colorée dans MATLAB est de taille MxNx3, alors qu'une image en niveaux de gris est MxN. Cela signifie qu'il est plus rapide d'améliorer/modifier une image en niveaux de gris car il y a moins de données à suivre. Utilisez rgb2gray pour convertir l'image en niveaux de gris. (La fonction imrotate a été utilisée car nos photos étaient horizontales - cette ligne de code peut ou non être nécessaire dans votre version.)

• %convertir en niveaux de gris et faire pivoter
• I = imread(ControlFile);
• I = rgb2gris(I);
• I = imroter (I, 90);

Ensuite, affichez l'image. La fonction de tracé secondaire est utilisée pour que l'image de test puisse être à côté du contrôle dans les étapes ultérieures.

• %affichage
• Figure 1);
• intrigue secondaire (1, 2, 1)
• imshow(I);
• titre(FichierContrôle);

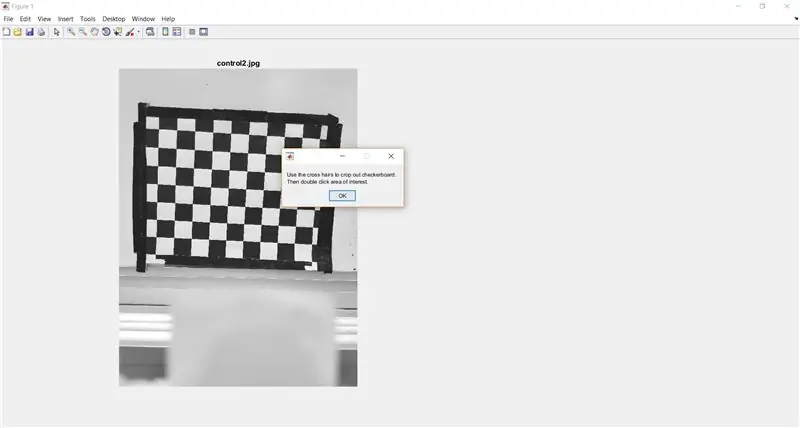
Utilisez imcrop pour inviter l'utilisateur à recadrer le damier de l'image complète. Le code suivant affiche également une boîte de message pour fournir des instructions à l'utilisateur.

• % rogner le damier pour l'analyse
• waitfor(msgbox({'Utilisez le réticule pour découper le damier.', 'Ensuite, double-cliquez sur la zone d'intérêt.'}));
• I_crop = imcrop(I);

Utilisez imbinarize pour binariser l'image.

I_binaire = imbinarize(I_crop);

Étape 4: Calculez la largeur des carrés blancs sur le damier

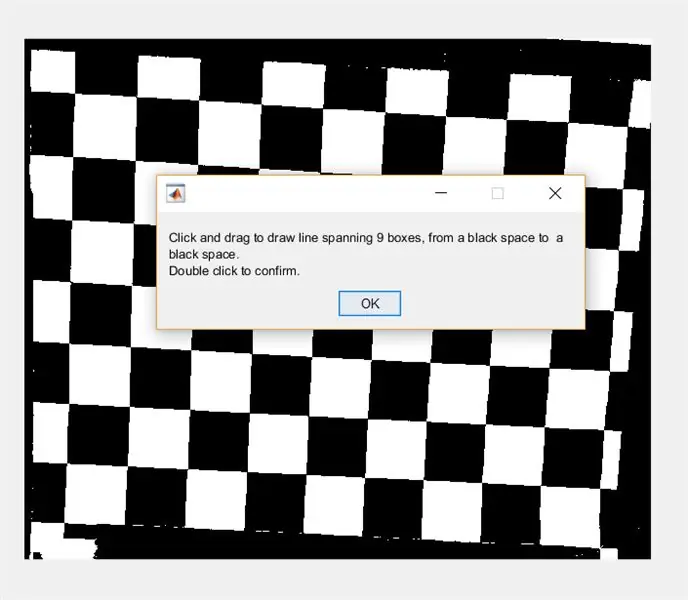
Ensuite, invitez l'utilisateur à tracer une ligne sur l'image à l'aide de imline. Cette ligne doit traverser horizontalement le damier. Il devrait commencer et se terminer sur un carré noir (peu importe où) - c'est parce que nous allons mesurer la largeur des carrés blancs, pas les noirs.

• %dessiner une ligne
• Figure 1)
• intrigue secondaire (1, 2, 1)
• imshow(I_binaire);
• waitfor(msgbox({'Cliquez et faites glisser pour tracer une ligne couvrant 9 cases, d'un espace noir à un espace noir.', 'Double-cliquez pour confirmer.'}));
• ligne = imline;
• position = attendre(ligne);
• points de terminaison = line.getPosition;

Extrayez les coordonnées X et Y des extrémités de la ligne tracée.

• X = points finaux (:, 1)
• Y = points de terminaison(:, 2);

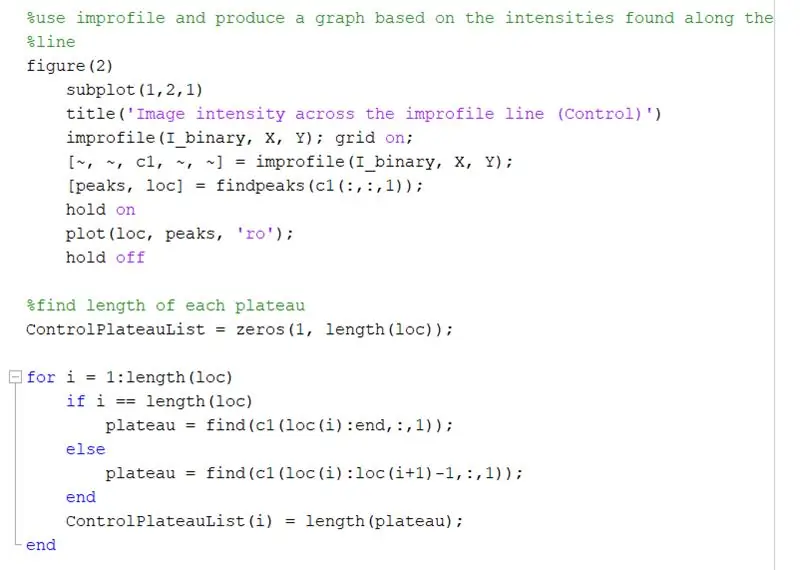
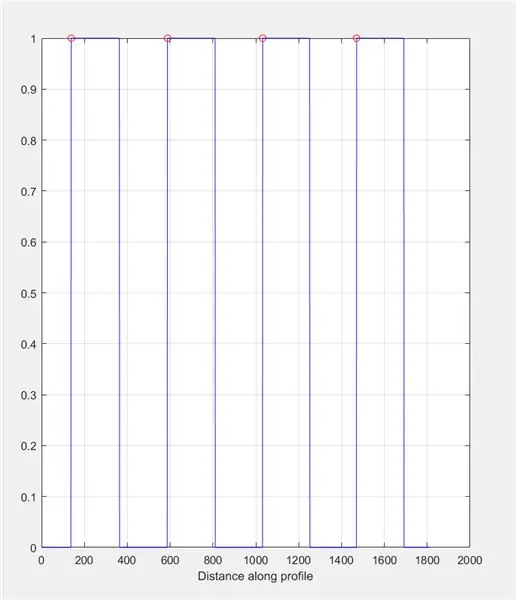
Utilisez improfile pour produire un graphique basé sur les intensités trouvées le long de la ligne tracée. Cela devrait ressembler à une onde carrée allant de 0 (noir) à 1 (blanc). Calculez également les sommets et leurs emplacements.

• Figure 2)
• intrigue secondaire (1, 2, 1)
• title('Intensité de l'image à travers la ligne d'improfile (Contrôle)')
• improfile(I_binaire, X, Y); grille allumée;
• [~, ~, c1, ~, ~] = improfile(I_binaire, X, Y);
• [pics, loc] = findpeaks(c1(:,:, 1));
• attendez
• plot(loc, pics, 'ro');
• retenir

Trouvez la longueur de chaque plateau sur le graphique d'improfile à l'aide d'une boucle for. Exécutez la boucle for pour le même nombre de pics qu'il y a dans le graphique improfile. Pour calculer la longueur de chaque plateau, utilisez la fonction « trouver » pour trouver tous les emplacements où il y a une valeur d'intensité « 1 » au lieu d'une « 0 ». Ensuite, calculez la longueur de ce tableau pour obtenir la longueur totale du plateau, qui doit être égale à la largeur d'un carré blanc en pixels. ControlPlateauList = zeros(1, length(loc));

pour i = 1: longueur(loc)

si je == longueur(loc)

plateau = find(c1(loc(i):end,:, 1));

autre

plateau = trouver(c1(loc(i):loc(i+1)-1,:, 1));

finir

ControlPlateauList(i) = longueur(plateau);

finir

Étape 5: Répétez les étapes 3 et 4 pour l'image de test

*Remarque: lorsque vous tracez la ligne improfile sur l'image de test, assurez-vous de la tracer à travers les carrés qui correspondent à la ligne que vous avez tracée sur l'image de contrôle.

Étape 6: Calculez le grossissement de l'objectif

Les mesures agrandies sont calculées en divisant la moyenne de la longueur du plateau, qui a été calculée à l'étape 5, par la moyenne de la longueur du plateau de contrôle, qui a été calculée à l'étape 4. Ceci est calculé à 1,0884.

grossissement = moyenne(plateauList)/mean(ControlPlateauList);

Étape 7: Recherche de R-carré et de la prescription de l'utilisateur via l'interpolation

Utilisation du code:

• md1 = fitlm(Prescription donnée, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Nous pouvons trouver la valeur R au carré du graphique GivenPresciption (nos objectifs ont des valeurs données) par rapport à MagArray (un tableau des rapports de mesures de grossissement que nous avons calculés précédemment). En ayant une valeur R au carré suffisamment élevée, on peut en déduire qu'il existe une corrélation suffisamment forte pour justifier l'utilisation de cette méthode. Pour ce cas particulier, la valeur R au carré était de 0,9912, ce qui suggère une forte corrélation et justifie donc l'utilisation de cette méthode dans l'analyse.

Utilisation de la fonction:

Prescription = interp1(MagArray, GivenPrescription, grossissement, 'linéaire');

Nous pouvons interpoler la valeur de prescription correspondante (sur l'axe des x) de notre rapport de grossissement (une valeur sur l'axe des y) et trouver quelle est la prescription de l'utilisateur.

L'interpolation des données est importante pour que cette méthode fonctionne car elle nous permet de faire des hypothèses sur les informations que nous n'avons pas, sur la base des informations dont nous disposons. Alors qu'une ligne de meilleur ajustement serait techniquement un candidat plus fort pour cette hypothèse, la création de limites pour réduire le nombre de sorties a le même effet que les verres correcteurs ont de toute façon des valeurs uniformes incrémentielles. Ceci est expliqué dans les étapes ultérieures.

Étape 8: Affichage de la prescription de l'utilisateur sur un graphique

En utilisant le code suivant:

• chiffre;
• plot(GivenPrescription, MagArray, '-g')
• attendez
• plot(Prescription, grossissement, 'pb')
• retenir
• la grille
• legend('Données', 'Points interpolés', 'Emplacement', 'NW')

Nous pouvons tracer un graphique qui montre les rapports de grossissement par rapport à la prescription donnée avec une ligne verte et les données trouvées de notre grossissement calculé par rapport à notre prescription interpolée avec une étoile bleue. Ensuite, la légende étiquette le titre, l'axe des x et l'axe des y et place la légende dans le coin supérieur gauche.

Étape 9: affinez votre ordonnance

Le code suivant est utilisé pour produire l'arrondi de la prescription:

• si Prescription <= 1,125

  Prescription Calculée = '1.0';

• elseif Prescription <= 1,375

  Prescription Calculée = '1.25';

• elseif Prescription <= 1,625

  Prescription calculée = '1,5';

• elseif Prescription <= 1,875

  Prescription calculée = '1.75';

• elseif Prescription <= 2,25

  Prescription Calculée = '2.0';

• elseif Prescription <= 2,625

  Prescription calculée = '2,5';

• elseif Prescription <= 3

  Prescription calculée = '2,75';

• elseif Prescription <= 3,375

  Prescription Calculée = '3.25';

• autre

  Prescription calculée = 'inconnu';

• finir

La prescription trouvée par interpolation ne reflète pas nécessairement la prescription réelle - c'est parce qu'il y aura toujours de légères variations dans l'analyse de la photo en raison d'une erreur humaine. Ainsi, nous avons besoin de cette étape pour classer la prescription réelle.

Les prescriptions qui sont données commencent généralement à partir de 1,0 dioptrie et augmentent de 0,25 dans leurs prescriptions, donc après avoir calculé la prescription, nous voulons déterminer la prescription qui convient le mieux à ce dont l'utilisateur pourrait avoir besoin. Après avoir calculé la prescription, nous la passons en revue les instructions If données pour vérifier sa valeur et déterminer quelle prescription est nécessaire. Tout ce qui est inférieur ou égal à 1,125, alors la prescription est de 1,0. Tout ce qui est inférieur ou égal à 1,375, la prescription est de 1,25. Tout ce qui est inférieur ou égal à 1,625, la prescription est de 1,5. Tout ce qui est inférieur ou égal à 1,845, la prescription est de 1,75. Etc.

Nous avons les valeurs croissantes puisque nous vérifions si les valeurs sont inférieures à. Si nous faisions diminuer les valeurs, la première instruction if lirait la première instruction if tout le temps. Si la prescription est la plus petite, nous voulons qu'elle la reconnaisse immédiatement comme la plus petite, c'est pourquoi la plus petite valeur est ce avec quoi nous avons commencé. Tout ce qui est supérieur à la valeur la plus élevée signifie que la prescription n'est pas dans la plage de nos données, elle donnera donc la lecture de chaîne « Inconnu ».