Module de pilotage laser DIY pour Arduino : 14 étapes (avec photos)

2024 Auteur: John Day | [email protected]. Dernière modifié: 2024-01-30 09:09

Dans ce Instructable, je vais démontrer la construction d'un module de direction de faisceau laser à double axe et à miroir unique à l'aide de pièces imprimées en 3D et de composants peu coûteux d'eBay.

Ce projet présente des similitudes avec Arduino Laser Show avec contrôle XY complet et Arduino Laser Show avec Real Galvos, mais je pense qu'il est le premier à utiliser un design imprimé en 3D avec des solénoïdes peu coûteux. Je mets tous les fichiers de conception sous GPLv3 afin que la conception puisse être améliorée et améliorée.

Bien qu'à l'heure actuelle, j'ai seulement assemblé le module et écrit un code de test très basique, j'espère qu'un jour je pourrai passer au niveau supérieur en incorporant le code graphique vectoriel de mon précédent Instructable, Super Fast Analog Voltages d'Arduino.

Étape 1: Rassemblez les pièces imprimées non 3D

L'ensemble laser se compose des pièces suivantes:

• 4 micro solénoïdes
• Un miroir de 1/2 pouce
• Quatre vis M3

Les solénoïdes particuliers que j'ai utilisés ont été achetés sur eBay pour 1,45 $ chacun. Le miroir rond a été trouvé dans l'allée de l'artisanat chez HobbyLobby - un paquet de 25 m'a coûté moins de 3 dollars. Vous pouvez également trouver des miroirs sur eBay.

Vous aurez également besoin d'un pointeur laser bon marché, encore une fois, d'eBay. Un laser violet avec une feuille de vinyle phosphorescente est un excellent combo pour ce projet !

Un jeu de mains secourables n'est pas nécessaire, mais sera très utile pour tenir et positionner le pointeur laser. Un grand clip de reliure peut être utilisé pour maintenir le bouton d'alimentation enfoncé.

Vous aurez besoin d'un Arduino (j'ai utilisé un Arduino Nano) et d'un moyen de piloter les solénoïdes. Comme VajkF l'a déclaré dans les commentaires, vous pouvez utiliser des ponts en H préfabriqués tels que ceux basés sur le L298 ou le L9110. Ceux-ci sont facilement disponibles sur eBay pour quelques dollars et peuvent également être utilisés pour piloter des moteurs et des projets de robotique.

Comme je n'avais pas de pont en H, j'ai construit mon propre pilote à partir de composants discrets:

• Quatre transistors bipolaires NPN (j'ai utilisé un MPS3704)
• Quatre résistances (j'ai utilisé une résistance de 1,2 kohm)
• Quatre diodes (j'ai utilisé un 1N4004)
• Une pile 9V et un connecteur de batterie

Les composants électroniques provenaient de mon laboratoire, je n'ai donc pas de coût exact pour eux, mais à moins que vous n'ayez déjà les pièces ou que vous puissiez les récupérer, il est probablement plus rentable d'utiliser un pont en H pré-construit. Néanmoins, je vais fournir les schémas pour construire le vôtre.

Étape 2: Imprimez en 3D le module de direction miroir

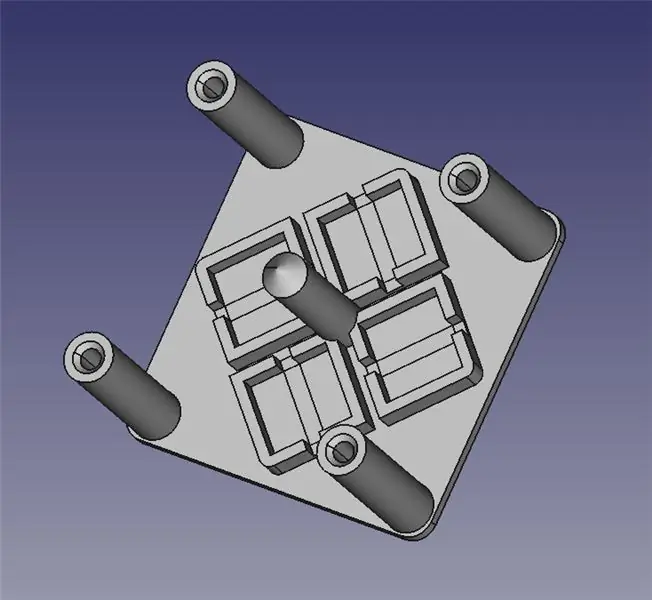
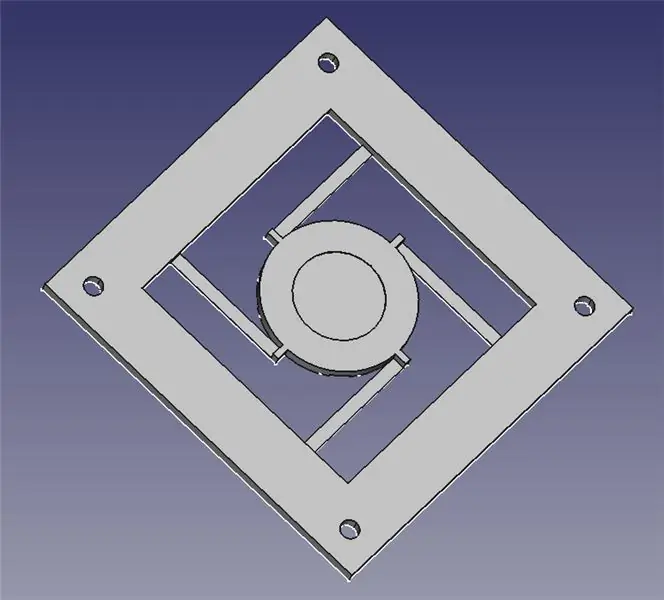
Le module de pilotage laser se compose de deux pièces imprimées en 3D: une base pour le montage de quatre solénoïdes et une plate-forme articulée pour le miroir.

J'ai joint les deux fichiers STL pour l'impression 3D, ainsi que les fichiers FreeCAD au cas où vous auriez besoin de modifier la conception. Tout le contenu est sous GPLv3, vous êtes donc libre d'apporter et de partager vos améliorations !

Étape 3: Assembler le module laser

• Utilisez de la colle chaude pour fixer les quatre solénoïdes à la pièce inférieure.
• Utilisez de la colle chaude pour fixer le miroir au centre de la pièce supérieure.
• Insérez les pistons métalliques dans les solénoïdes puis positionnez la pièce supérieure sur les poteaux (mais ne la vissez pas). Tournez légèrement la pièce supérieure et à l'aide d'un petit tournevis, soulevez chaque piston en position. La lèvre du disque doit glisser dans la rainure du piston. Attention, les charnières imprimées en 3D sont très fragiles. Avec de la patience et éventuellement quelques tentatives infructueuses, vous devriez pouvoir positionner les quatre pistons sans tordre ni exercer de pression sur les charnières.
• Une fois tous les pistons positionnés, insérez partiellement les vis M3, mais avant de les serrer, appuyez doucement sur chaque piston et assurez-vous que le miroir s'incline librement. S'il ne bouge pas librement ou s'accroche, il peut être nécessaire de retirer la plaque supérieure, de soulever un ou plusieurs solénoïdes et de le rattacher légèrement vers l'extérieur (mettre des entretoises entre elle et le poteau central peut aider à cela).

Étape 4: Imprimez le collier du pointeur laser

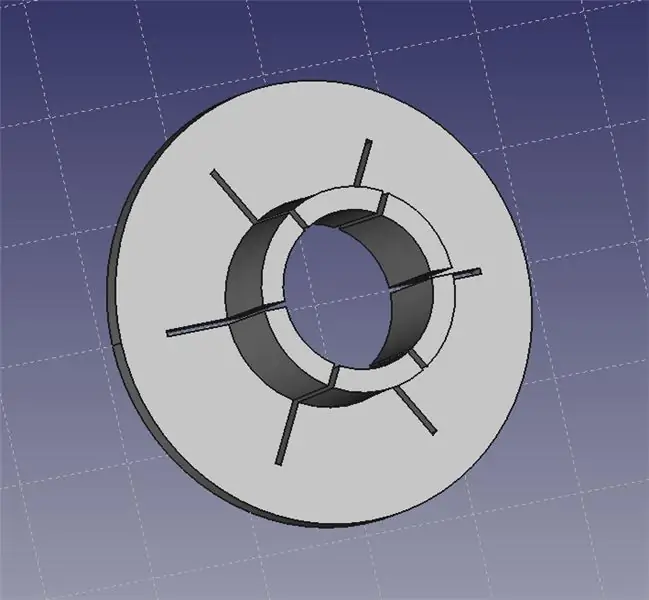
Le collier du pointeur laser s'adapte sur la tête du pointeur laser. Vous pouvez ensuite utiliser un jeu de mains secourables pour saisir le collier et vous permettre de positionner précisément le laser sur votre banc.

Étape 5: Assembler le circuit de conduite

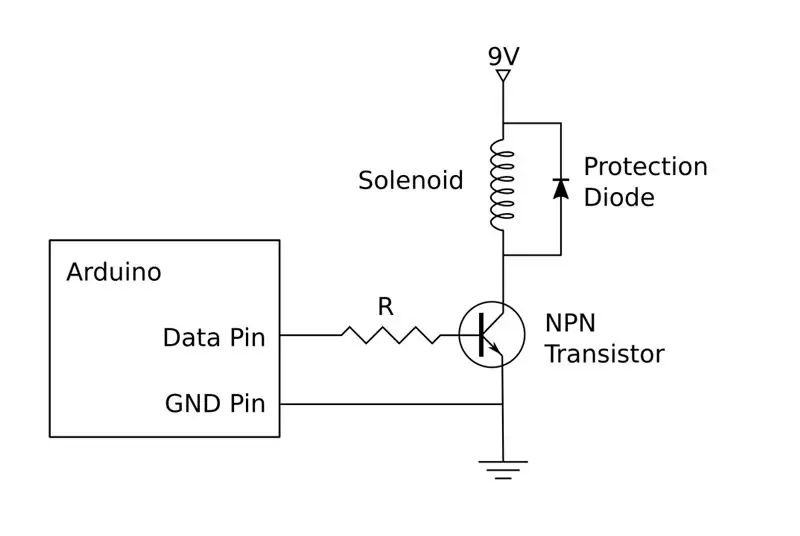
Le circuit d'entraînement est représenté sur le schéma. Comme indiqué précédemment, ma version est construite à partir de composants discrets, mais vous pouvez également utiliser un pont en H facilement disponible. Si vous choisissez de construire le vôtre, vous devrez construire quatre copies de ce circuit, une pour chacun des quatre solénoïdes.

Chaque circuit se connectera à une broche Arduino, deux pour contrôler les solénoïdes gauche et droit et deux pour les solénoïdes haut et bas. Ceux-ci devront être connectés à des broches compatibles PWM, comme ceci:

• Broche 9: Solénoïde vers le haut
• Broche 3: solénoïde vers le bas
• Broche 11: Solénoïde gauche
• Broche 10: Solénoïde droit

Une seule batterie 9V peut être utilisée pour piloter les quatre circuits de commande de solénoïde ou vous pouvez utiliser une alimentation de table. L'Arduino fonctionnera sur alimentation USB et ne doit pas être connecté au côté positif de la batterie 9V. Cependant, le côté négatif de la batterie est utilisé comme référence de masse et doit être câblé à la broche GND de l'Arduino ainsi qu'aux broches de l'émetteur des transistors.

Étape 6: Téléchargez l'exemple de code

L'exemple de code a été mis à jour avec les fonctionnalités suivantes:

• Ajuste la fréquence PWM de telle sorte que le mécanisme soit presque silencieux à basse vitesse. Le bourdonnement du Motion Test 1 a complètement disparu !
• Ajoute comme équations de tension basées sur l'article de Schimpf afin de "linéariser" la réponse non linéaire des solénoïdes.

J'ai également inclus une implémentation d'un Lorenz Attractor basé sur le code de ce blog.

La fidélité des résultats laisse un peu à désirer, mais j'y travaille encore !:)

Les étapes suivantes illustrent certaines des techniques utilisées dans le code.

Étape 7: Baisser le volume

Dans mon Motion Test 1, vous pouvez entendre un fort bourdonnement, en particulier lors des mouvements de haut en bas. Il s'avère que cela était dû au fait que la fréquence de découpage PWM par défaut de l'Arduino se situait dans la plage audible. La commutation rapide de la tension de la bobine les ferait vibrer à cette fréquence, les transformant en minuscules haut-parleurs.

Pour résoudre ce problème, j'ai augmenté la fréquence PWM dans le code:

#define PWM_FREQ_31372Hz 0x01 // Définit la fréquence PWM à 31372.55 Hz#define PWM_FREQ_3921Hz 0x02 // Définit la fréquence PWM à 3921.16 Hz #define PWM_FREQ_980Hz 0x03 // Définit la fréquence PWM à 980.39 Hz void setPWMuint8_TC (fréquence 1B & 0b11111000) | la fréquence; // Régler la fréquence du timer1 (broches 9 & 10) TCCR2B = (TCCR2B & 0b11111000) | la fréquence; // Régler la fréquence du timer2 (broches 3 et 11) }

Le réglage de la fréquence Arduino PWM est une astuce utile pour calmer les solénoïdes ou les moteurs. Expérimentez avec les différents choix de fréquences pour voir laquelle vous donne les meilleurs résultats. Bien que cela implique une programmation plus avancée, une bonne ressource sur le fonctionnement des minuteries se trouve ici.

Étape 8: Réglage des tensions pour réduire la distorsion

Mes premiers tests de mouvement ont montré qu'il y avait une distorsion significative dans la réponse des solénoïdes. Dans Motion Test 3 (figure de gauche), ce qui était censé être une spirale circulaire est devenu à la place une toile rectangulaire avec des bords déchiquetés.

Résoudre ce problème nécessitait un peu de mathématiques, mais j'ai pu localiser un article étonnant sur le Web qui m'a aidé à comprendre suffisamment le problème pour le résoudre par logiciel.

Ce qui suit vous guide tout au long du processus que j'ai suivi pour régler le système et améliorer l'apparence des traces résultantes !

Étape 9: Perfectionner le logiciel, avec les mathématiques

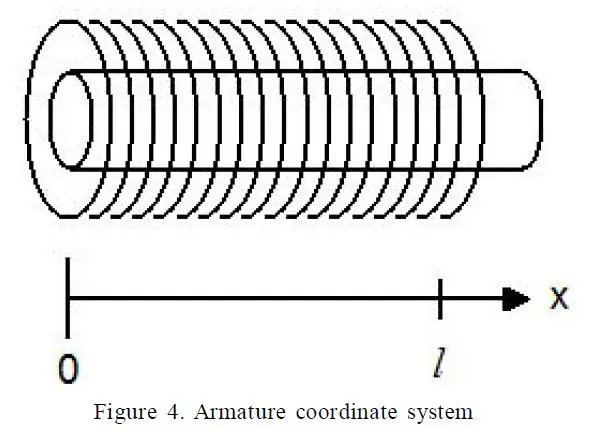
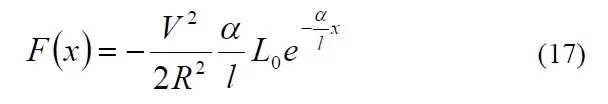
Le secret pour régler le système s'est avéré être un excellent article intitulé "A Detail Explanation of Solenoid Force" par Paul H. Schimpf de l'Eastern Washington University (lien). En particulier, l'équation 17 m'a donné la force du solénoïde en termes de divers termes.

Les termes suivants étaient faciles à mesurer:

• R - La résistance de mon solénoïde
• l - La longueur du solénoïde
• x - Le déplacement du piston dans le solénoïde
• V - La tension aux bornes du solénoïde

Je savais aussi que la force émise par le solénoïde devait équilibrer la force des ressorts imprimés en 3D sur le miroir à double axe. La force d'un ressort est régie par la loi de Hooke, qui s'énonce comme suit:

F = -kx

Bien que je ne connaisse pas la valeur de k, je savais au moins que la force que je tirais de l'équation 17 de l'article de Schimpf devait être égale à la force de la loi de Hooke.

La valeur de alpha (α) était délicate. Bien que les équations 13 et 14 aient montré comment calculer ces valeurs à partir de la surface du solénoïde (A), du nombre de tours (N) et des valeurs de perméabilité magnétique (μ), je ne voulais pas avoir à déchirer un solénoïde pour compter le nombre de tours, et je ne connaissais pas non plus le matériau à partir duquel le noyau de mon solénoïde était fabriqué.

Étape 10: Un testeur de composants bon marché sauve la mise

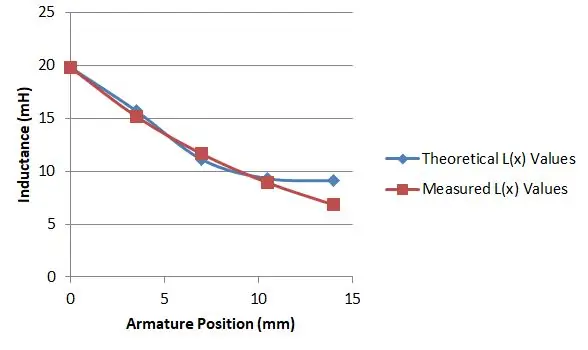
Il s'est avéré cependant que les équations 15 et 16 m'ont donné ce dont j'avais besoin. J'avais un testeur de composants M328 bon marché que j'avais acheté sur eBay pour 10 $. Il a pu l'utiliser pour mesurer l'inductance de mon solénoïde et j'ai découvert qu'en poussant l'armature à différentes profondeurs, cela me donnait différentes valeurs d'induction.

Le mesurer avec l'armature complètement insérée m'a donné la valeur de L(0).

La longueur de mon solénoïde était de 14 mm, j'ai donc mesuré l'inductance avec l'armature à cinq positions et cela m'a donné différentes valeurs pour L(x):

• L(0,0) = 19,8 mH
• L(3,5) = 17,7 mH
• L (7,0) = 11,1 mH
• L (10,5) = 9,3 mH
• L(14) = 9,1 mH

J'ai ensuite utilisé une feuille de calcul pour tracer mes valeurs par rapport à la valeur des équations 15 et 16, pour un choix particulier de r, puis j'ai varié mon choix jusqu'à ce que je trouve une bonne correspondance. Cela s'est produit lorsque μr était de 2,9, comme le montre le graphique.

Étape 11: Trouvez la constante de ressort K, résolvez le problème

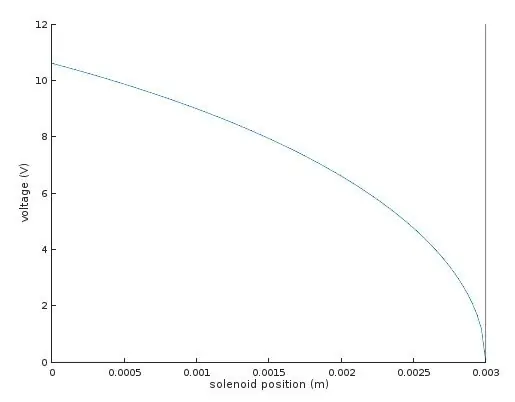
La seule inconnue restante était K, la constante de ressort. J'ai mesuré cela en appliquant 9V à l'un des solénoïdes de mon assemblage à deux axes et en mesurant la distance à laquelle le miroir a été abaissé. Avec ces valeurs, j'ai pu résoudre les équations pour K, que j'ai trouvées autour de 10,41.

J'avais maintenant les valeurs dont j'avais besoin pour calculer la traction du solénoïde à différentes positions le long de la course. En définissant F(x) égal à la force du ressort de la loi de Hooke, je peux résoudre la tension requise V.

Le graphique montre la tension requise pour déplacer le solénoïde à n'importe quelle position souhaitée x.

A droite, où la tension est nulle et la position est de 3 mm, cela correspond au point de repos neutre du solénoïde lorsque les charnières imprimées en 3D sont complètement relâchées. Se déplacer vers la gauche sur le graphique correspond à tirer l'armature dans le solénoïde contre la traction des charnières imprimées en 3D - cela nécessite initialement plus de tension, mais à mesure que l'armature s'enfonce plus profondément dans le solénoïde, la traction augmente et la tension d'entraînement requise diminue.

Cette relation est définitivement non linéaire, mais avec les équations de l'article de Schimpf, je peux écrire mon code Arduino pour produire les tensions correctes afin que la déviation du faisceau soit linéaire:

float positionToVoltage(float x) {

// Force de restauration exercée par les charnières (loi de Hooke) à x désiré. const float spring_F = -spring_K * (x - spring_X0); // Tension telle que la force de traction du solénoïde correspond à la // force de rappel des charnières return sqrt(-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp(-a*x/solenoid_len))); }

Cela conduit à une spirale beaucoup plus circulaire que dans mon test de mouvement d'origine. Mission accomplie!

Étape 12: Questions et réponses sur le circuit de commande utilisant des composants discrets

Pourquoi ne puis-je pas connecter le solénoïde directement à l'Arduino ?

Il s'agit de la quantité de courant que l'Arduino peut fournir sans subir de dommages. C'est environ 40mA par broche. Sachant que l'Arduino fonctionne à 5V, nous pouvons utiliser la loi d'Ohm pour calculer la résistance minimale requise de la charge (dans ce cas, le solénoïde). Diviser 5 volts par 0,040 ampères nous donne 125 ohms. Si la charge a une plus grande résistance, nous pouvons la connecter directement à l'Arduino, sinon nous ne le pouvons pas. Un petit solénoïde a généralement une résistance de 50 ohms, nous ne pouvons donc pas le piloter directement depuis l'Arduino. Si nous le faisions, il tirerait 100 mA, ce qui est clairement trop.

Pourquoi utilisez-vous 9V pour le solénoïde, mais 5V pour l'Arduino ?

L'Arduino fonctionne à 5V, mais c'est un peu trop peu pour un solénoïde. L'utilisation d'un transistor nous permet de choisir une tension pour le solénoïde qui est indépendante du 5V utilisé pour l'Arduino.

Comment savoir si un transistor convient à ce projet ?

Tout comme l'Arduino, la principale exigence est que le courant traversant le solénoïde ne dépasse pas les valeurs nominales maximales du transistor (en particulier, le courant du collecteur). Nous pouvons facilement calculer le pire des cas en mesurant la résistance du solénoïde, puis en divisant la tension d'alimentation par celle-ci. Dans le cas d'un courant d'alimentation de 9 V pour les solénoïdes et d'une résistance de solénoïde de 50 ohms, le pire des cas nous place à 180 mA. Le MPS3704, par exemple, est conçu pour un courant collecteur maximum de 600 mA, ce qui nous donne une marge d'environ 3.

Comment déterminer la valeur minimale de la résistance à mettre entre la sortie de l'Arduino et la base du transistor ?

La sortie de l'Arduino connectera la jambe de base des transistors bipolaires à travers une résistance de limitation de courant. Puisque l'Arduino fonctionne à 5V, nous pouvons à nouveau utiliser la loi d'Ohm pour calculer la résistance nécessaire pour limiter le courant en dessous de 40mA. Autrement dit, divisez 5 volts par 0,04 ampère pour obtenir une valeur d'au moins 125 ohms. Des valeurs de résistance plus élevées diminueront le courant, nous donnant ainsi une marge de sécurité encore plus grande.

Y a-t-il une valeur maximale pour cette résistance que je ne devrais pas dépasser ?

Il s'avère que oui. Un transistor a ce qu'on appelle un gain de courant. Par exemple, si le gain est de 100, cela signifie que si nous mettons 1 mA dans la base, jusqu'à 100 mA traverseront la charge que le transistor contrôle. Si nous mettons 1,8 mA dans la base, jusqu'à 180 mA traverseront la charge. Puisque nous avons calculé plus tôt qu'à 9V, 180mA traverse le solénoïde, alors un courant de base de 1,8mA est le "point idéal", et moins et notre solénoïde ne s'allumera pas complètement.

Nous savons que l'Arduino émet 5V et nous voulons que 1,8mA de courant circule, nous utilisons donc la loi d'Ohm (R=V/I) pour calculer la résistance (R=V/I). 5V divisé par 1,8mA donne une résistance de 2777 ohms. Donc, étant donné les hypothèses que nous avons faites, nous nous attendons à ce que la résistance se situe entre 125 et 2777 - choisir quelque chose comme 1000 ohms nous donne une assez bonne marge de sécurité dans tous les cas.

Étape 13: Analyse des problèmes actuels et solutions possibles

Le prototype actuel montre du potentiel, mais plusieurs problèmes subsistent:

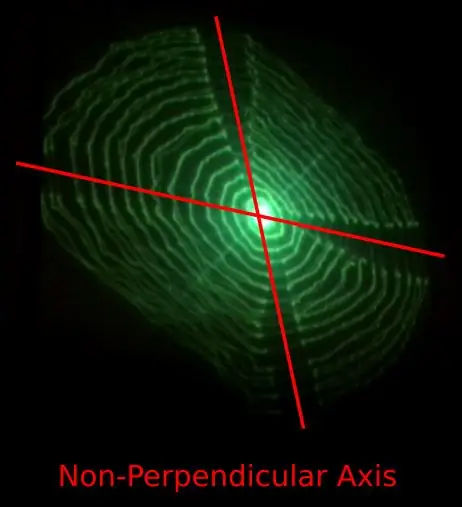
1. Le mouvement le long des axes X et Y ne semble pas perpendiculaire.
2. Il y a un saut lorsque le miroir change de direction.
3. La résolution est assez faible et il y a des motifs de marches d'escalier visibles.
4. À des vitesses de mouvement plus élevées, la trajectoire du laser est déformée par les vibrations et la sonnerie.

Le problème 1) peut être causé par la conception des charnières flexibles imprimées en 3D qui transmettent le mouvement le long d'un axe à l'axe perpendiculaire.

Le problème 2) est dû à un jeu dans l'accouplement entre les pistons d'entraînement et la plate-forme du miroir, ce qui provoque des secousses et des sauts du miroir aux transitions entre les axes X et Y. Ce mouvement soudain conduit à un espace en forme de X assombri où le point laser effectue un mouvement incontrôlé plus rapide.

Le problème 3) se produit parce que l'Arduino PWM par défaut n'a que 255 niveaux et bon nombre d'entre eux sont gaspillés en raison de la forme de la courbe de tension. Cela pourrait être considérablement amélioré par l'utilisation de timer1, qui est de 16 bits et serait capable de 65536 valeurs uniques.

Le problème 4) se produit parce que le miroir et l'armature coulissante du solénoïde (pistons) constituent une quantité importante de masse en mouvement.

Comme les problèmes 1) et 2) sont liés à la conception mécanique, une possibilité peut être de retirer les pistons métalliques et de les remplacer par de petits aimants aux terres rares qui sont fixés directement sur la plaque d'inclinaison. Les solénoïdes seraient une bobine ouverte qui attirerait ou repousserait les aimants sans établir de contact physique. Cela conduirait à un mouvement plus fluide et éliminerait la possibilité de secousses, tout en réduisant la masse totale.

La réduction de la masse est la principale solution pour le problème 4), mais tous les problèmes restants pourraient être ciblés directement dans le logiciel en implémentant un profil de contrôle de mouvement dans le logiciel pour accélérer et décélérer le miroir de manière contrôlée. Cela est déjà largement fait dans le micrologiciel de l'imprimante 3D et des méthodes similaires pourraient également fonctionner ici. Voici quelques ressources liées au contrôle de mouvement tel qu'il s'applique aux imprimantes 3D:

• "Mathématiques des profils de contrôle de mouvement", Chuck Lewin (lien)
• "Jerk Controlled Motion Explained", (lien)

Je soupçonne que l'ajout d'un profil de contrôle de mouvement trapézoïdal permettrait au miroir d'être entraîné à des vitesses beaucoup plus élevées sans artefacts de sonnerie ou de vibration.

Étape 14: Travaux futurs et applications possibles

Bien que le développement de solutions à ces problèmes demande un travail considérable, j'espère que ce module de pilotage de faisceau open source pourra devenir une alternative abordable aux projets basés sur le galvanomètre dans des applications telles que:

• Un spectacle laser bon marché pour DJ et VJ.
• Un affichage vectoriel électromécanique pour un jeu d'arcade vintage tel que le Vectrex.
• Une imprimante 3D SLA de type résine DIY qui, dans l'esprit du mouvement RepRap, peut imprimer son propre module de pilotage laser.
• Panoramique numérique ou stabilisation optique de l'image pour les appareils photo.

Deuxième prix au concours Arduino 2017