☠WEEDINATOR☠ Partie 4 : Code de géométrie de direction différentielle : 3 étapes

2024 Auteur: John Day | [email protected]. Dernière modifié: 2024-01-30 09:09

Si vous avez le temps de regarder la vidéo ci-dessus, vous remarquerez qu'il y a des bruits étranges causés par les moteurs de la direction qui calent de temps en temps alors que le WEEDINATOR effectue un virage à 3 points. Les moteurs se bloquent essentiellement les uns contre les autres car le rayon de braquage est différent de l'intérieur vers l'extérieur et la distance parcourue par la roue est différente par degré de tour.

La géométrie du virage peut être élaborée en esquissant environ 8 permutations du virage, en donnant des exemples de virages à différents angles sur la roue intérieure de 0 (pas de virage) à 90 (verrouillage complet) degrés. Cela semble compliqué?

La plupart des petits robots à roues n'essaient pas d'avoir une direction sophistiquée et s'appuient, très efficacement, sur le simple changement de la vitesse relative des moteurs de chaque côté du véhicule, ce qui est à peu près la même chose qu'une pelle ou un char à chenilles. travaux. C'est génial si vous chargez au-dessus d'une zone de guerre remplie de cratères en tirant sur tout ce qui bouge, mais dans un environnement agricole tranquille, il est important de faire le moins de dégâts possible au sol et au sol afin que les meules d'avant en arrière l'une contre l'autre soient non approprié!

La plupart des voitures et des tracteurs ont un gadget très utile appelé « Différentiel », à l'exception des voitures que vous voyez dans les vieux films américains où vous pouvez entendre les pneus grincer comme des fous à chaque fois qu'ils tournent au coin de la rue. Les Américains construisent-ils encore des voitures comme celle-ci ? Avec le WEEDINATOR, nous pouvons programmer le différentiel dans les moteurs d'entraînement en élaborant la formule pour les vitesses et les angles relatifs des roues à n'importe quel angle de braquage particulier. Cela semble toujours compliqué?

Voici un exemple rapide:

Si le WEEDINATOR effectue un virage et que sa roue intérieure est à 45 degrés, la roue extérieure n'est PAS à 45 degrés, c'est plutôt à 30 degrés. De plus, la roue intérieure peut tourner à 1 km/heure, mais la roue extérieure sera nettement plus rapide, plutôt à 1,35 km/heure.

Étape 1: Configuration de la géométrie

Quelques hypothèses de base sont faites pour commencer:

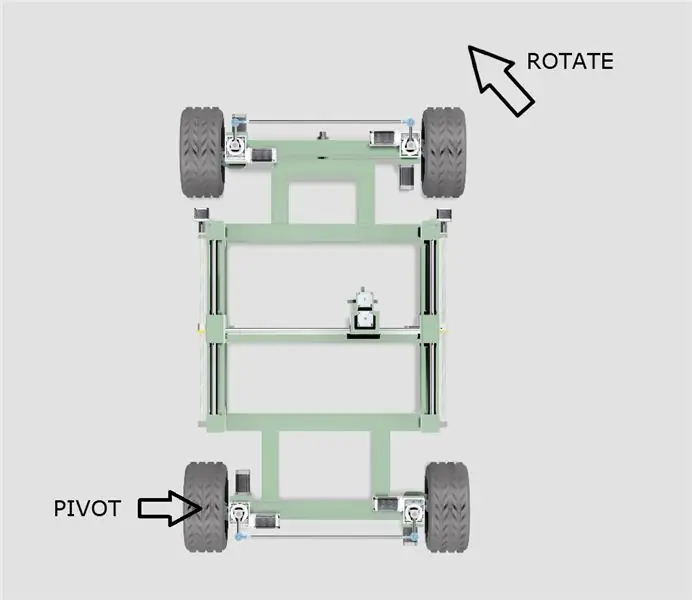
• Le châssis pivotera autour d'une des roues arrière comme indiqué sur le schéma ci-dessus.
• Le centre effectif du cercle de pivot se déplacera le long d'une ligne prolongée à partir des centres des deux roues arrière, en fonction de l'angle de virage.
• La géométrie prendra la forme d'une courbe sinusoïdale.

Étape 2: Dessins à l'échelle des angles et des rayons des roues

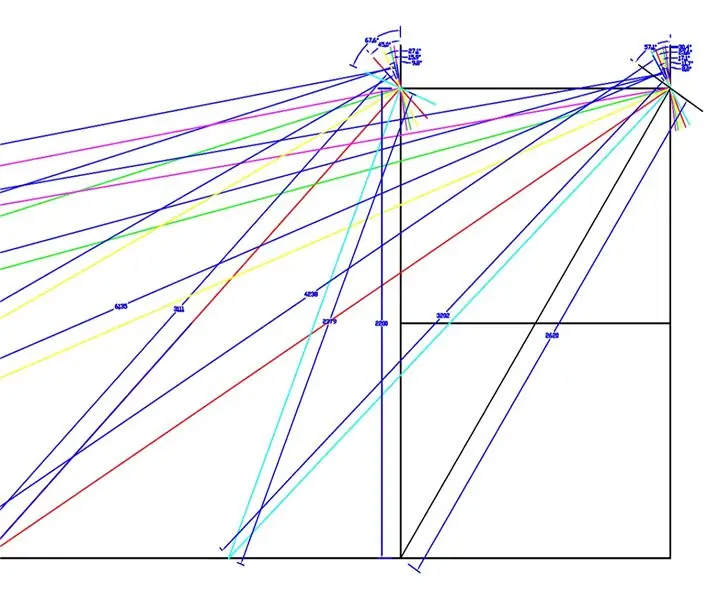
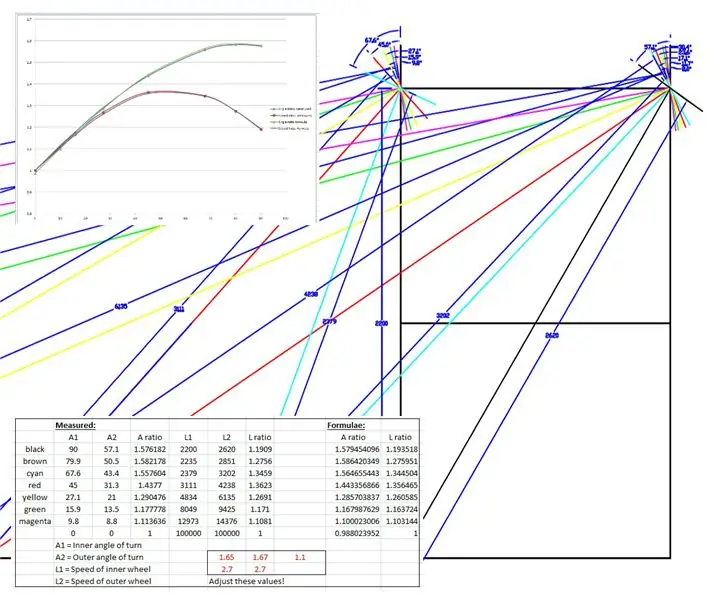
Un dessin à grande échelle a été réalisé pour les roues avant et le châssis du WEEDINATOR avec 8 permutations différentes d'angle de roue intérieur entre 0 et 90 degrés et les centres de virage respectifs ont été cartographiés comme indiqué dans les dessins ci-dessus.

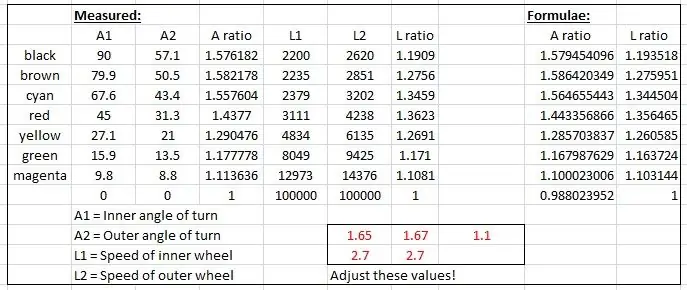
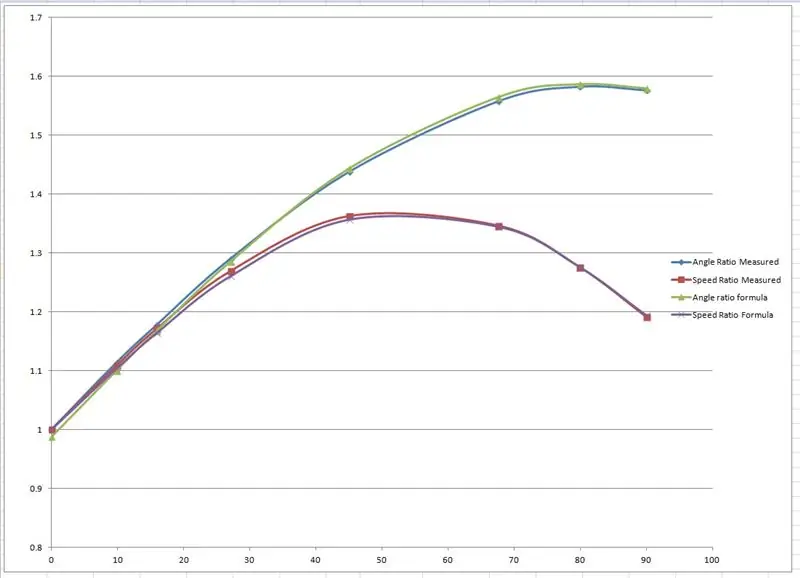
Les rayons effectifs ont été mesurés à partir du dessin et tracés sur un graphique dans Microsoft Excel.

Deux graphiques ont été produits, l'un pour le rapport des essieux des roues avant gauche et droite et un autre pour le rapport des deux rayons pour chaque angle de braquage particulier.

J'ai ensuite "truqué" certaines formules pour imiter les résultats empiriques basés sur une courbe sinusoïdale. L'un des truquages ressemble à ceci:

speedRatio= (sin(interne*1.65*pi/180)+2.7)/2.7; // intérieur est l'angle de virage intérieur.

Les courbes ont été falsifiées en modifiant les valeurs affichées en rouge dans le fichier Excel jusqu'à ce que les courbes s'emboîtent.

Étape 3: Codage des formules

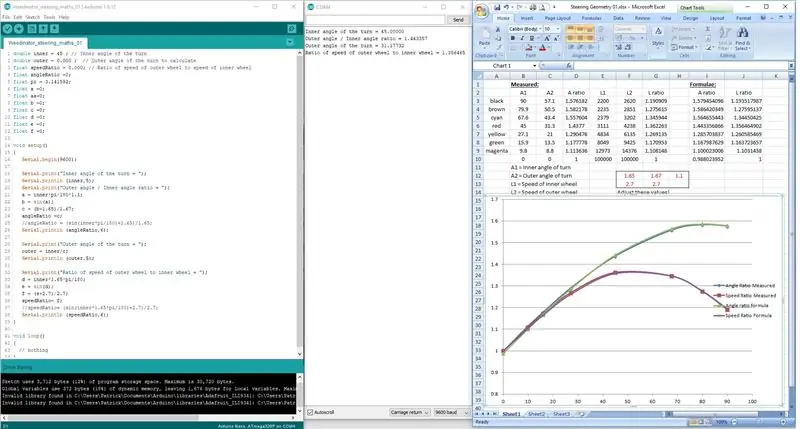
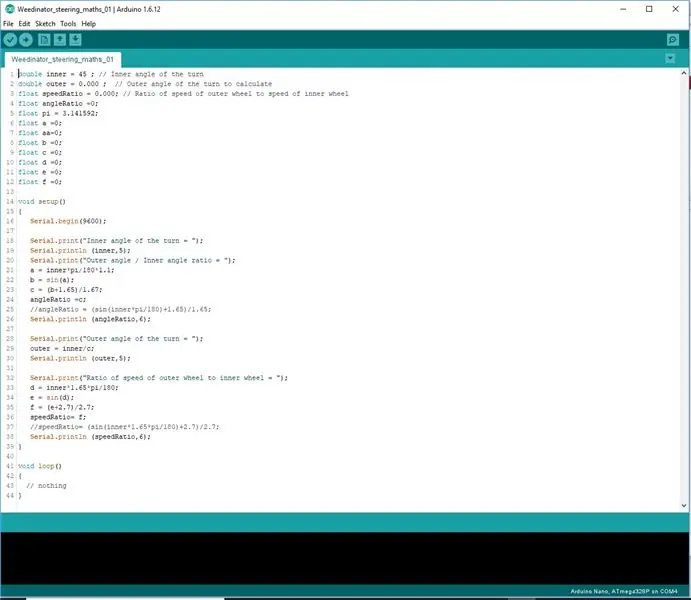
Plutôt que d'essayer de coder les formules sur une seule ligne, elles ont été décomposées en 3 étapes pour permettre à l'Arduino de traiter correctement les calculs.

Les résultats sont affichés sur l'affichage du port série et vérifiés avec les résultats mesurés sur le dessin à l'échelle.