Table des matières:
- Étape 1: Comprendre les tables de vérité
- Étape 2: Connaître les symboles
- Étape 3: Formater le tableau
- Étape 4: Attribuer Vrai et Faux
- Étape 5: Négation
- Étape 6: Variable « q »
- Étape 7: Résolution des faux dans la dernière colonne
- Étape 8: Trouver le vrai dans la dernière colonne
- Étape 9: Finir la table
- Étape 10: Terminé
- Auteur John Day day@howwhatproduce.com.
- Public 2024-01-30 09:05.
- Dernière modifié 2025-01-23 14:45.

Une table de vérité est un moyen de visualiser tous les résultats d'un problème. Ce jeu d'instructions est conçu pour les personnes qui débutent en mathématiques discrètes. Nous allons nous exercer aujourd'hui avec un exemple de problème spécifique à ces instructions. Vous aurez besoin de papier brouillon et d'un crayon pour visualiser le tableau. Ce problème devrait prendre environ 5 minutes pour les personnes ayant des connaissances préalables sur le sujet et environ 10 minutes pour les débutants.
Pour ce jeu d'instructions, nous nous concentrerons sur le problème ~p Λ q. Nous l'utilisons pour introduire certains symboles nécessaires à l'interprétation des tables de vérité.
Étape 1: Comprendre les tables de vérité

Une table de vérité est un moyen de visualiser toutes les possibilités d'un problème. Connaître les tables de vérité est une nécessité fondamentale pour les mathématiques discrètes. Ici, nous allons trouver tous les résultats pour l'équation simple de ~p Λ q.
Étape 2: Connaître les symboles

La première étape vers la table de vérité consiste à comprendre les signes. Le "~" dans ce problème particulier représente la négation. Le « p » et le « q » sont tous deux des variables. Le « Λ » est équivalent à « et ». Cette équation est lue comme "pas p et q", ce qui signifie que l'équation est vraie si p n'est pas vrai et q est vrai.
Étape 3: Formater le tableau

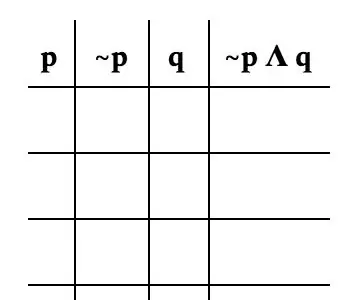
Maintenant pour former la table réelle. Il est important de décomposer le problème par chaque variable. Pour ce problème, nous allons le décomposer comme suit: p, ~p, q et ~p Λ q. L'image est un bon exemple de ce à quoi devrait ressembler votre table.
Étape 4: Attribuer Vrai et Faux

Puisqu'il n'y a que deux variables, il n'y aura que quatre possibilités par variable. Pour p, nous le découpons avec la moitié des espaces pris par T (pour vrai) et l'autre moitié par F (pour faux).
Étape 5: Négation

Pour ~p, vous écrivez le signe opposé de p puisque ~p est l'opposé de p.
Étape 6: Variable « q »

Pour q, vous alternez entre T et F afin d'obtenir chaque combinaison possible. Étant donné que l'équation se concentre uniquement sur ~p, nous pouvons ignorer la colonne p lors de la détermination de la vérité de l'équation. Le symbole « Λ » signifie que ~p et q doivent être vrais pour que l'équation soit vraie.
Étape 7: Résolution des faux dans la dernière colonne

Pour la première ligne, puisque ~p est F et q est T, ~p Λ q est F dans le scénario où ~p est F et q est T. Le seul scénario où l'équation est T est où ~p est T et q est T.
Étape 8: Trouver le vrai dans la dernière colonne

Cela signifie que la seule ligne qui est T est la troisième.
Étape 9: Finir la table

Vérifiez que votre table est correcte. Pour ce faire, vérifiez que vos signes sont corrects et assurez-vous que la dernière colonne est effectuée correctement. La dernière colonne est le résultat de toutes les permutations possibles à partir des variables.
Étape 10: Terminé
Maintenant que vous savez comment faire une table de vérité de base, continuez à vous entraîner ! Plus vous pratiquerez, mieux vous les ferez.
Conseillé:
Routeur WIFI sécurisé - Protection et confidentialité contre les virus, les logiciels malveillants et les ransomwares : 5 étapes

Routeur WIFI sécurisé - Protection et confidentialité contre les virus, les logiciels malveillants et les ransomwares : Protection des points de terminaison à faible coût à l'aide de RaspBerryPI 4 et de l'open source. Bloque les éléments suivants AVANT qu'ils n'atteignent votre ordinateur ou votre téléphone : via la publicité
ET OU PAS !! (Table de vérité interactive) : 4 étapes

ET OU PAS !! (Interactive Thruth Table) : Hé les gars, j'espère que vous allez tous bien chez vous et que vous vous demandez quoi bricoler avec les matériaux disponibles ?? Ne vous inquiétez pas, cet article vous aidera sûrement en construisant un circuit simple !! Comprendre les portes logiques est très important à la fois pour le
Gérez 100 appareils dans les applications, les organisations, les rôles et les utilisateurs Ubidots : 11 étapes

Gérer 100 appareils dans les applications, les organisations, les rôles et les utilisateurs d'Ubidots : à cette occasion, j'ai décidé de tester la fonctionnalité de la plate-forme IoT Ubidots pour la gestion des utilisateurs dans le cas où elle aurait de nombreux appareils pour plusieurs organisations ou entreprises sous la même Plateforme Ubidots. Information du maire : vous
Comment résoudre le problème de broche 3,3 V dans les disques en marque blanche extraits des disques Western Digital Easystore de 8 To : 6 étapes

Comment résoudre le problème de broche 3,3 V dans les disques en marque blanche extraits des disques Western Digital 8 To Easystore : Si vous trouvez cette instruction utile, veuillez envisager de vous abonner à ma chaîne Youtube pour les prochains tutoriels de bricolage concernant la technologie. Merci
Comment résoudre les problèmes avec la télécommande au volant Pionner - Augmentez le signal IR et réparez le petit verrouillage.: 14 étapes

Comment résoudre les problèmes avec la télécommande au volant Pionner - Augmentez le signal IR et réparez le petit verrouillage. : Cette télécommande est très belle et pratique, mais parfois ne fonctionne pas correctement. projet n'est pas un exemple d'efficacité. Je viens du Brésil et j'ai trouvé cette astuce sur Amaz
